欢迎查看我的公众号原文

细嗦Transformer（二）: Attention及FFN等细节部分解读和代码实现
也欢迎关注我的公众号：

Q1: **Transformer为何使用多头注意力机制？**

使用Multi-Head，主要是为了：

① 捕捉不同的特征，每个头可以学习到输入序列不同方面的特征或模式。

② **增强模型的表达能力，**多个头的并行计算可以丰富模型的表达能力，使其能够关注到输入的不同方面。

多头注意力机制计算过程中，每个头都有自己的权重矩阵，最后再将每个头的输出拼接起来，进行线性变换，从而使模型能够综合利用多个头的信息。

Attention注意力机制

对注意力机制的理解，简单来讲就是，一句话中的一个词，只与句中的部分词有关系，而不是与每个词都有关系，attention就是衡量这种关系程度的一种方式。如下图所示：

Attention函数是将一个query和一组键值对(key-value)映射到输出output,这里的都是向量。Output输出是值Values的加权和。

Scaled Dot-Product Attention

论文中将注意力称为Scaled Dot-Product Attention，也就是缩放的点积注意力。这个注意力的计算方式为：公式的输入包含维度为的和，以及维度为的，然后将一个与其他全部进行点积运算，每次的计算结果除于，经过一次运算后再与进行点积运算。对每一个都需要进行同样的操作。

计算公式为：$$Attention(Q,K,V)=softmax(\frac{Q{K}^T}{\sqrt{d_k}})V$$
熟记这个公式
Softmax计算公式为：$$softmax(x)=\frac{e^{x_i}}{{\sum }_i{e}^{x_i}}$$，将值压缩到$[0,1]$之间。

Q2: 为什么要除以 ?

1. 论文中有说，当较大时，可能会变得非常大，导致函数的梯度变得非常小，进而导致梯度消失。
2. 计算结果是一个一维向量，每个元素表示单个token的值，当过大时，可能导致某一个元素的非常大，进而在经过计算后，部分值趋近于0，部分值趋近于1，导致模型难以学习到有效注意力。

接下来对这个过程进行图解，主要参考：The Illustrated Transformer

QKV计算方式

上文所说的和和的计算方式如下图所示。这里以输入“Thinking Machines”为例

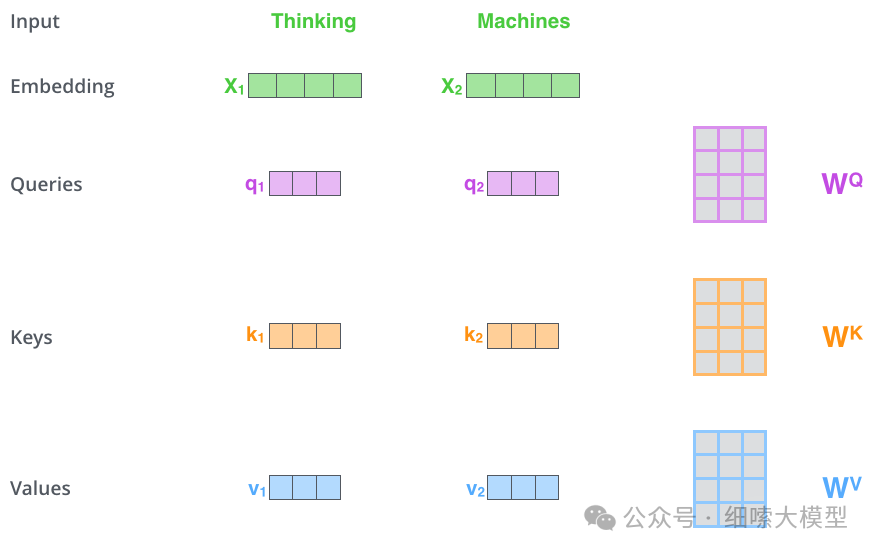
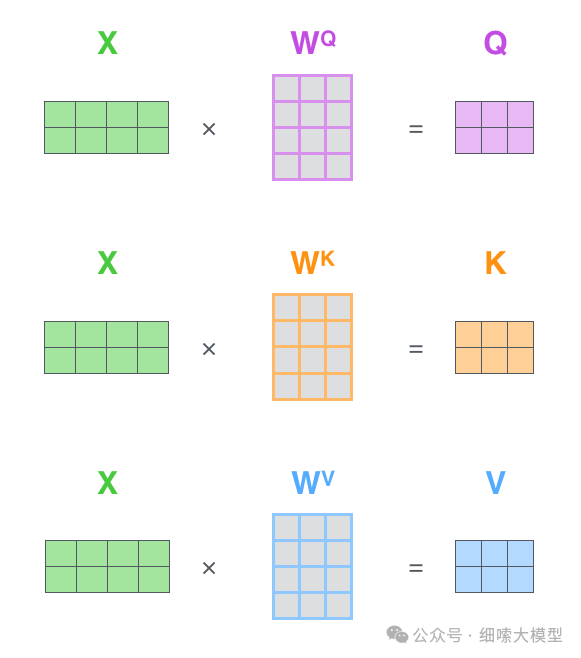
注意：

在Embedding的时候，一个token是embbeding成维的向量，如果输入的token长度为4096，一个token embedding成，那么输入层Embedding之后的维度为维，是一个矩阵。如果batch为4，那么输入层的Embedding结果就为。还需要注意图中的"Thinking Machines"是为了简单起见，当成一个token来处理，实际上这里还有一步tokenize的过程。

如上图所示，输入向量，经过与矩阵相乘，得到，，的计算过程一样，这里的是模型通过训练学习到的矩阵参数。

有了之后，其中的计算过程如下图所示。

$q_1$与$k_1,k_2$分别进行点击运算，然后除于$\sqrt{(d_k)}$，这里$d_k$就是$key$的维度，论文中的维度为64，$\sqrt{(d_k)}=8$，所以图中除的是8。除以 $\sqrt{(d_k)}$ 可以使梯度更加稳定。然后再经过一个$Softmax$得到向量[0.88,0.12]，最后于$value(v_1)$进行点积运算，得到$q_1$的输出$z_1$。

因此，Self-Attention层的公式就表示为：

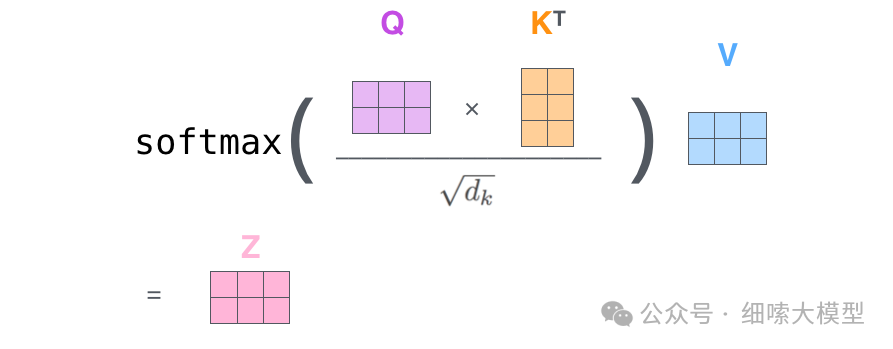
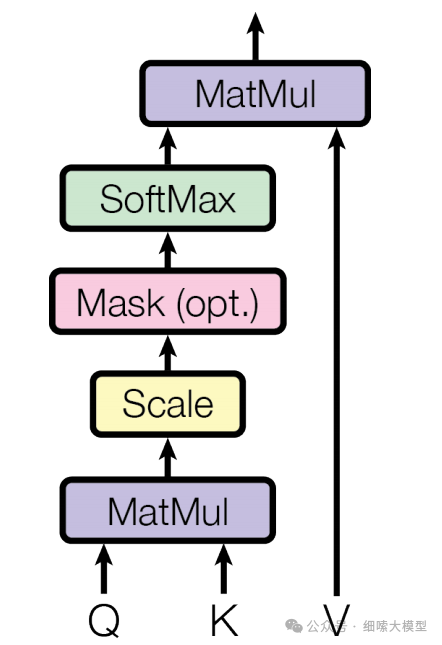
Attention代码实现

def attention(query, key, value, mask=None, dropout=None):
    breakpoint()
    "Compute 'Scaled Dot Product Attention'"
    d_k = query.size(-1)
    scores = torch.matmul(query, key.transpose(-2, -1)) / math.sqrt(d_k) # [1,8,10,64] * [1,8,64,10] -> [1,8,10,10]
    if mask is not None:
        scores = scores.masked_fill(mask == 0, -1e9)
    p_attn = scores.softmax(dim=-1)
    if dropout is not None:
        p_attn = dropout(p_attn)
    return torch.matmul(p_attn, value), p_attn

Q3: 代码中的mask的作用是什么？为什么要做mask操作？

主要是对padding部分进行mask。padding就是为了让输入序列保持相同的长度，以便在同一个batch中进行计算，而在序列后面填充的特殊标记，通常为0。因此，padding部分是不带有任何语义，也不需要参与注意力计算的，所以需要在计算注意力的得分之前，将padding部分mask掉，通常是将padding位置的得分设为一个非常大的负数，通过softmax后，这些位置的权重接近于0，从而不影响实际有效的token序列。

在上面的代码块中，体现在第7行。

Multi-Head Attention多头注意力机制

多头注意力机制，简单的讲就是有多个不同的$Q,K,V$。

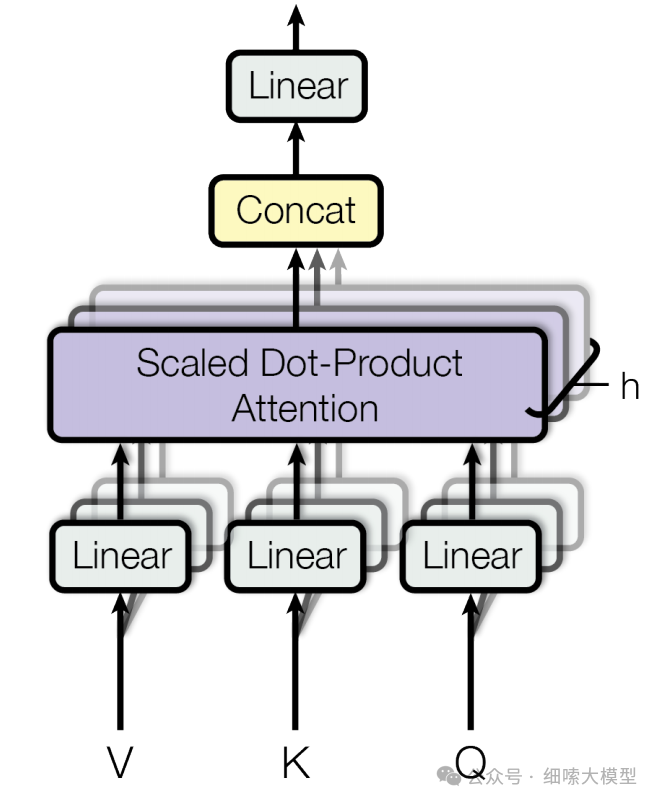
多头注意力机制，简单的讲就是有多个不同的$Q,K,V$。

使用了组结构相同但参数不同的自注意力模块$W^Q,W^K,W^V$

每组查询$Query$、键$Key$和值$Value$的映射构成一个“头”，并独立地计算自注意力的运算

最后，不同头的输出被拼接在一起，并通过一个权重矩阵$W^O\in R^{H\ast H}$进行映射，产生最终的输出。

计算公式为：
$$\begin{gathered} \mathrm{MultiHead}(Q,K,V)=\mathrm{Concat}(\mathrm{hea}{\mathrm{d}}_1,...,\mathrm{hea}{\mathrm{d}}_{\mathrm{h}})W^O \\ \text{where}\mathrm{hea}{\mathrm{d}}_{\mathrm{i}}=\mathrm{Attention}(Q{W}_i^Q,K{W}_i^K,V{W}_i^V) \end{gathered}$$
其中,$W_i^Q\in {\mathbb{R}}^{d_{\text{model}}\times d_k}$, $W_i^K\in {\mathbb{R}}^{d_{\text{model}}\times d_k}$, $W_i^V\in {\mathbb{R}}^{d_{\text{model}}\times d_v}$ and $W^O\in {\mathbb{R}}^{h{d}_v\times d_{\text{model}}}$.

根据前面注意力公式，单个注意力的输出$z$的维度为$[d_{model},d_v]$，也就是token数量乘以$value$的维度。注意，按照论文中所述，$query,key$的维度不一定与的维度相同。以前面给出的示例为例，Thinking Machines的经过单个注意力模块输出的结果为，维度为$2\ast 3$：，那么经过8个注意力模块后，就有8个维度相同的输出，如下图所示：

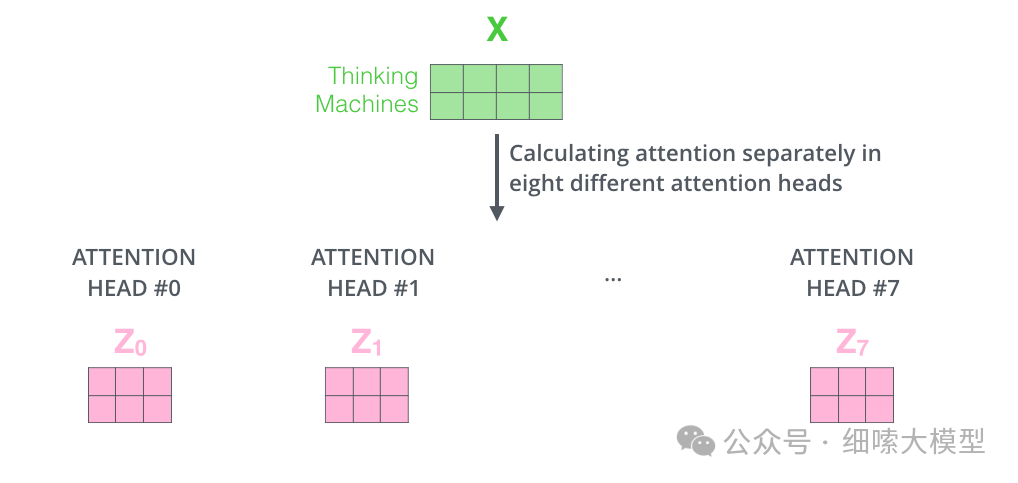
那么这里存在的一个问题就是，全连接层无法接受多个矩阵，只能接受单个矩阵。因此，在每个注意力模块计算完成之后，再将全部计算经过进行一次拼接，再与一个权重矩阵$W_O$相乘，映射到维度为：$[d_{model},d_v]$的矩阵。如下图所示：

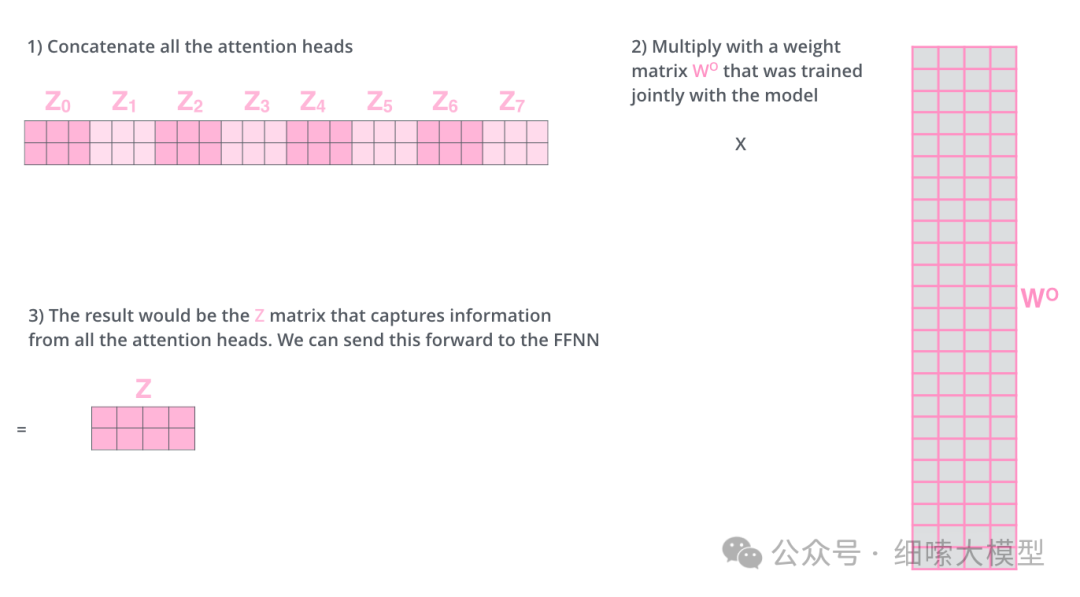
用一张图来表示多头注意力机制的计算过程如下：

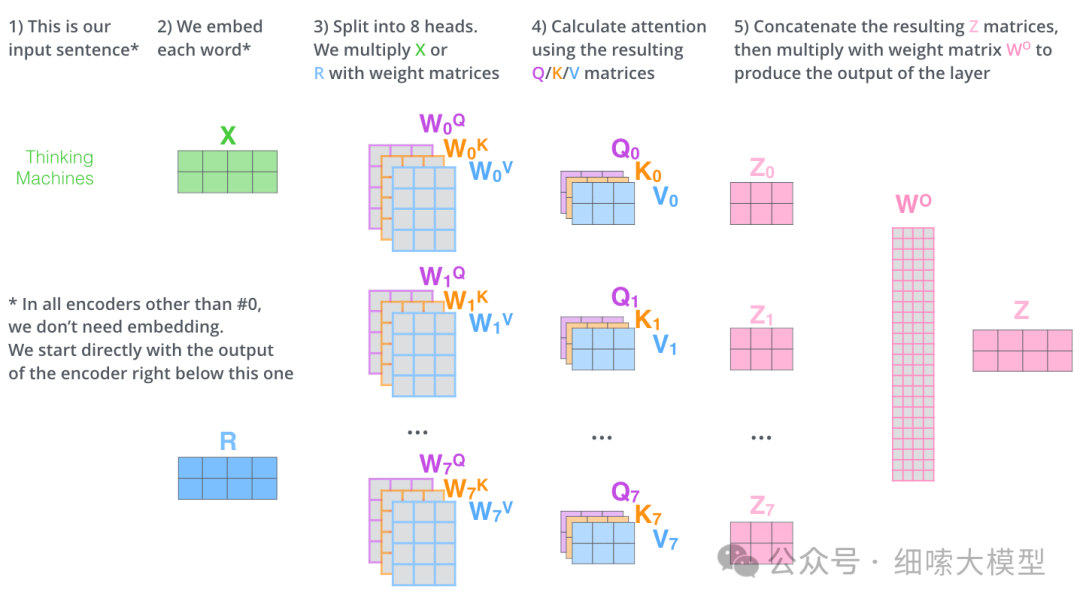
Multi-Head Attention代码实现

class MultiHeadedAttention(nn.Module):
    def __init__(self, h, d_model, dropout=0.1):
        "Take in model size and number of heads."
        super(MultiHeadedAttention, self).__init__()
        assert d_model % h == 0
        # We assume d_v always equals d_k
        self.d_k = d_model // h
        self.h = h
        self.linears = clones(nn.Linear(d_model, d_model), 4)
        self.attn = None
        self.dropout = nn.Dropout(p=dropout)

    def forward(self, query, key, value, mask=None):
        "Implements Figure 2"
        breakpoint()
        # Encoder部分，mask输入维度为[1,1,10]
        if mask is not None:
            # Same mask applied to all h heads.
            mask = mask.unsqueeze(1) # [1,1,10] -> [1,1,1,10]
        nbatches = query.size(0)

        # 1) Do all the linear projections in batch from d_model => h x d_k
        query, key, value = [
            lin(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)
            for lin, x in zip(self.linears, (query, key, value))
        ] # [1, 10, 512] -> [1, 8, 10, 64], 8个头，每个头10个词，每个词64维

        # 2) Apply attention on all the projected vectors in batch.
        x, self.attn = attention(
            query, key, value, mask=mask, dropout=self.dropout
        )

        # 3) "Concat" using a view and apply a final linear.
        x = (
            x.transpose(1, 2)
            .contiguous()
            .view(nbatches, -1, self.h * self.d_k)
        )
        del query
        del key
        del value
        return self.linears[-1](x)

Q4: 为什么在进行多头注意力的时候需要对每个head进行降维？

在论文中， $h=8$每个注意力层有8个头，在每个注意力层中， . $d_k=d_v=d_{model/h}=64$因为减少每个head的维度，使总的计算量与单个head时的计算量相似。所以对每个head进行降维的主要目的是保证每个head的计算量不会太大的同时，通过多个head组合，增强模型的表达能力和鲁棒性。

Cross Attention Mechanism 交叉注意力机制

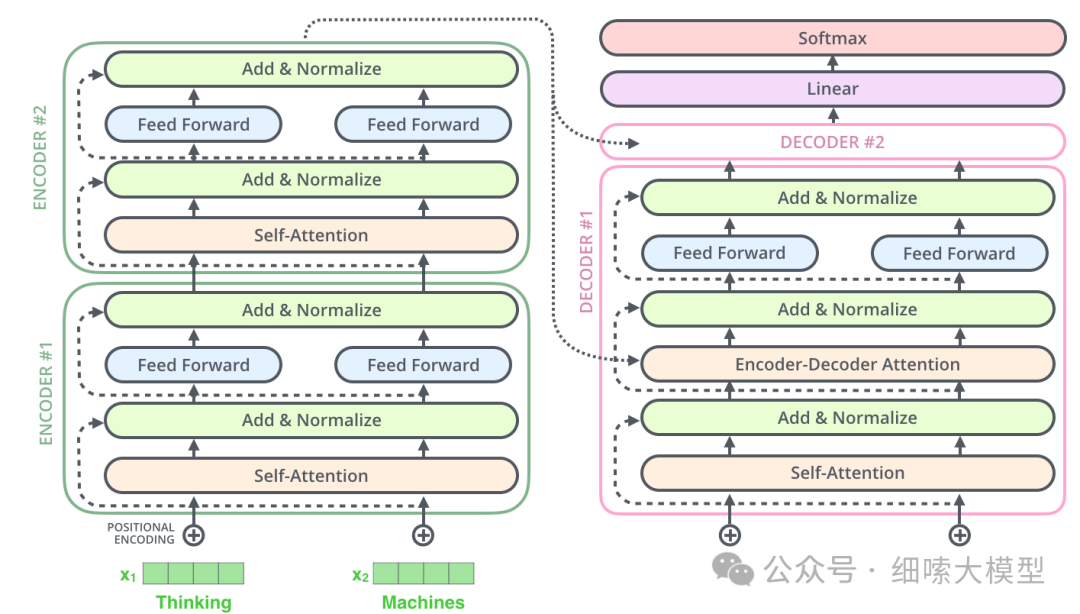
再回到下面这张Encoder-Decoder模型图中，可以看到，除了Encoder部分的多头注意力外，Encoder部分的输出，是输入到了Decoder的每一个注意力子层中。

最顶部的Encoder的输出，被转换成一组注意力向量，。

输出的将转递给Decoder中的每一个decoder层中交叉注意力模块使用，这有助于解码器专注于输入序列中的适当位置。

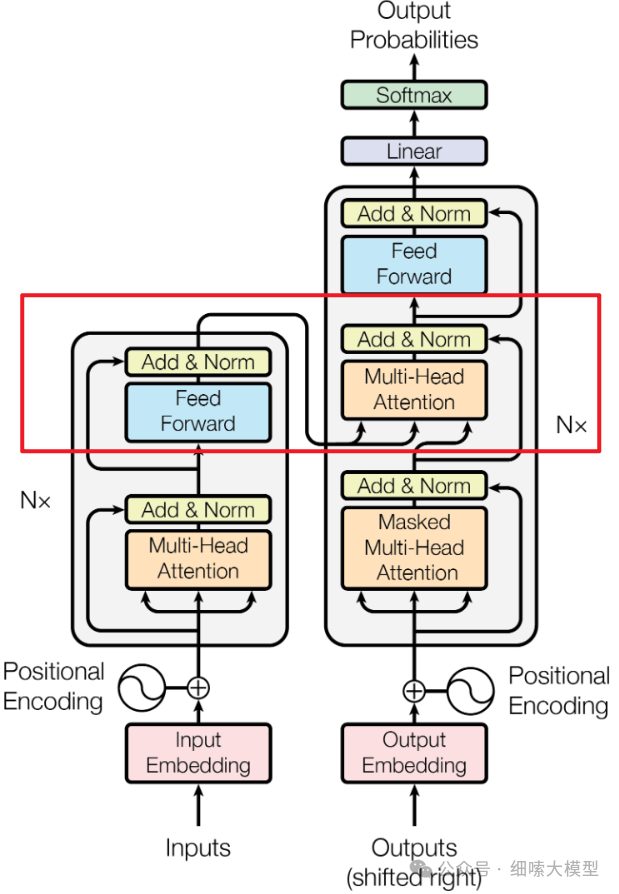
需要强调三点

1. Encoder输出的是
2. 只有最后一个encoder层的输出转给decoder
3. 是每一个decoder层都会收到来自encoder的

Masked Self-Attention掩码注意力机制

Decoder中的Self-Attention与编码器中的不同。因为Decoder的目的是基于前文预测下一个词，所以是不能让Decoder参考待预测词后文的，这里的注意力只能看到待预测词之前的文本。这就靠掩码注意力机制来实现，将待预测词之后的位置全部mask掉，设置成，再进行Self-Attention计算$-inf$，计算方式与Encoder中的一致。

如下图所示：

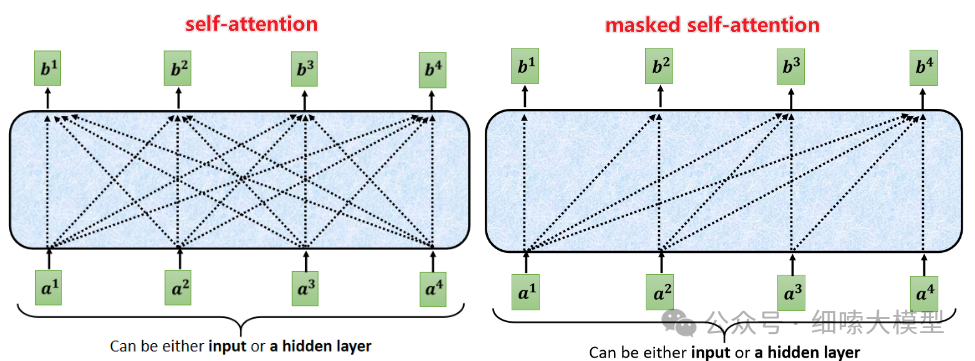
Position-wise Feed Forward Networks

每个encoder、decoder层中都包含有一个全连接前馈神经网络，在每个层中的位置相同。全连接层只有一个隐藏层，激活函数为。

计算公式为：$FFN(x)=max(0,x{W}_1+b_1)W_2+b_2$

全连接层的输入输出维度为，隐藏层的维度为：$d_{ff}=2048$

3

FFN代码实现

class PositionwiseFeedForward(nn.Module):
    "Implements FFN equation."

    def __init__(self, d_model, d_ff, dropout=0.1):
        super(PositionwiseFeedForward, self).__init__()
        self.w_1 = nn.Linear(d_model, d_ff)
        self.w_2 = nn.Linear(d_ff, d_model)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        return self.w_2(self.dropout(self.w_1(x).relu()))

Add & Norm 残差连接和层归一化

在每个encoder、decoder层中的每个子层后面，都需要经过残差连接和层归一化。

如下图所示：

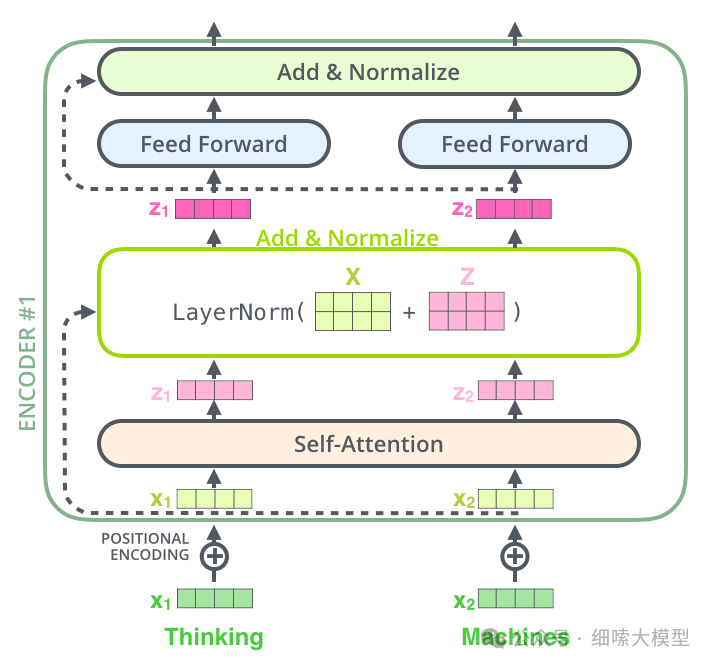
残差连接就是将层的输出加上输入，计算公式为：

层归一化将每一层神经元的输入都转成均值方差
LN 主要用于 NLP 领域，它对每个 token 的特征向量进行归一化计算。设某个 token 的特征向量为 $x\in {\mathbb{R}}^d$，LN 运算如下
$\mathrm{LN}(\mathbf{x})=\mathbf{\gamma }\odot \frac{\mathbf{x}-\hat{\mathbf{\mu }}}{\hat{\mathbf{\sigma }}}+\mathbf{\beta }$

.其中 $\odot$ 表示按位置乘， $\pmb{\gamma}, \pmb{\beta}\in \mathbb{R}^d $ 和 是 拉伸参数scale 和 偏移参数shift，代表着把第$i$个特征的 batch 分布的均值和方差移动到${\beta }^i,{\gamma }^i,\gamma$ 和 $\beta$ 是需要与其他模型参数一起学习的参数。$\hat{\mathbf{\mu }}$ ​ 和 $\hat{\boldsymbol{\sigma}} $ 表示特征向量所有元素的均值和方差，如下计算
$\hat{\mathbf{\mu }}=\frac{1}{d}{\sum }_{x^i\in \mathbf{x}}{x}^i$

${\hat{\mathbf{\sigma }}}^2=\frac{1}{d}{\sum }_{x^i\in \mathbf{x}}{\left(x^i-\hat{\mathbf{\mu }}\right)}^2+ϵ$

注意我们在方差估计值中添加一个小的常量，以确保我们永远不会尝试除以零。

给定一个包含有个token的句子，每个token表示出维的向量，LayerNorm要对每个token的向量进行归一化，共进行次归一化计算，如下图所示:

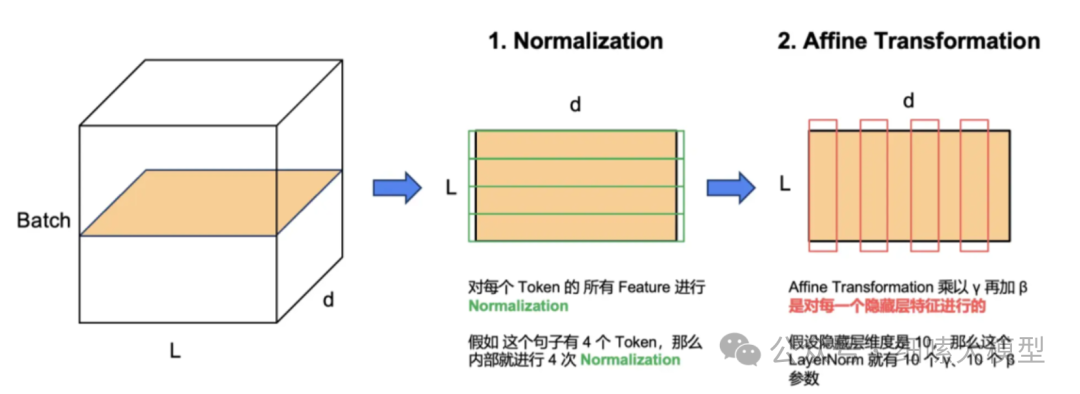
Add & Norm代码实现

class LayerNorm(nn.Module):
    "Construct a layernorm module (See citation for details)."

    def __init__(self, features, eps=1e-6):
        super(LayerNorm, self).__init__()
        self.a_2 = nn.Parameter(torch.ones(features))
        self.b_2 = nn.Parameter(torch.zeros(features))
        self.eps = eps

    def forward(self, x):
        mean = x.mean(-1, keepdim=True)
        std = x.std(-1, keepdim=True)
        return self.a_2 * (x - mean) / (std + self.eps) + self.b_2

Positional Encoding位置编码

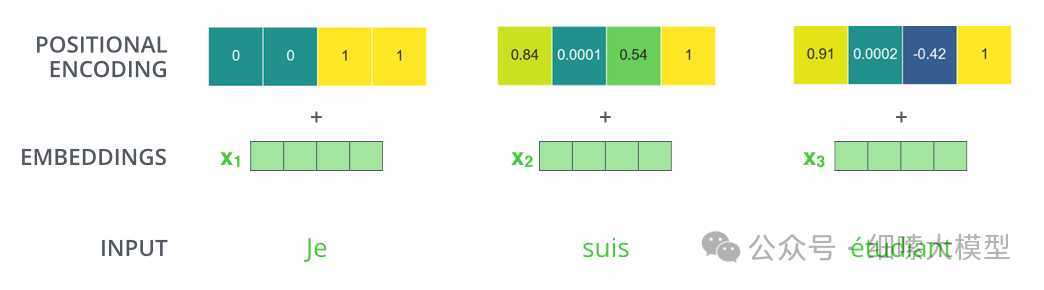
注意力机制能够学习到一个词与其他词的联系，但是无法学习到词与词之间的位置关系。所以，我们需要在Embedding层注入相对或绝对的位置关系。如下图所示，一个token除了编码成一个embedding向量外，还需要构建一个维度相同的向量，将两个向量相加作为Encoder的输入。加入了位置编码后，再映射到向量中，在进行Self-Attention计算时，就会考虑到距离关系。

位置编码的计算公式维：

其中表示位置，也就是第几个token，i表示这个token向量的第i维度，偶数位用，奇数位用。按照论文中所述，选取这个函数作为位置编码是因为这个函数允许模型相对容易的学习到位置关系，因为对于位置的token，相对于的任何偏移量的位置信息，都可以表示成相对于的线性函数。并且，允许模型在推理阶段处理更长的序列长度。

位置编码代码实现

class PositionalEncoding(nn.Module):
    "Implement the PE function."

    def __init__(self, d_model, dropout, max_len=5000):
        super(PositionalEncoding, self).__init__()
        self.dropout = nn.Dropout(p=dropout)

        # Compute the positional encodings once in log space.
        pe = torch.zeros(max_len, d_model)
        position = torch.arange(0, max_len).unsqueeze(1)
        div_term = torch.exp(
            torch.arange(0, d_model, 2) * -(math.log(10000.0) / d_model)
        )
        pe[:, 0::2] = torch.sin(position * div_term)
        pe[:, 1::2] = torch.cos(position * div_term)
        pe = pe.unsqueeze(0)
        self.register_buffer("pe", pe)

    def forward(self, x):
        x = x + self.pe[:, : x.size(1)].requires_grad_(False)
        return self.dropout(x)

6

Embedding代码实现

使用学习到的Embedding模型将输入输出部分的token编码成维$d_{model}$的向量，在Embedding层，还乘以$\sqrt{d_{model}}$。

class Embeddings(nn.Module):
    def __init__(self, d_model, vocab):
        super(Embeddings, self).__init__()
        self.lut = nn.Embedding(vocab, d_model)
        self.d_model = d_model

    def forward(self, x): # x: [1,10]
        return self.lut(x) * math.sqrt(self.d_model) # [1,10,512]

Q5: 为什么要对Embedding之后的词向量乘以 ?

为了保持向量的尺度稳定。Embedding的值通常是随机初始化的，乘以开方后的结果能保证在后续的点乘计算中，值的尺度不会过大或过小，从而有利于模型的训练稳定性。

测试

接下来测试整个模型的前向传播过程，结合上期讲到的代码，以及本期的全部代码，编写测试用例，查看模型最终的输出结果。

导包

import os
from os.path import exists
import torch
import torch.nn as nn
from torch.nn.functional import log_softmax, pad
import math
import copy
import time
from torch.optim.lr_scheduler import LambdaLR
import pandas as pd
import altair as alt
from torchtext.data.functional import to_map_style_dataset
from torch.utils.data import DataLoader
from torchtext.vocab import build_vocab_from_iterator
import torchtext.datasets as datasets
import spacy
import GPUtil
import warnings
from torch.utils.data.distributed import DistributedSampler
import torch.distributed as dist
import torch.multiprocessing as mp
from torch.nn.parallel import DistributedDataParallel as DDP

warnings.filterwarnings("ignore")
RUN_EXAMPLES = True

def show_example(fn, args=[]):
    if __name__ == "__main__" and RUN_EXAMPLES:
        return fn(*args)

构建模型

def make_model(
    src_vocab, tgt_vocab, N=6, d_model=512, d_ff=2048, h=8, dropout=0.1
):
    "Helper: Construct a model from hyperparameters."
    c = copy.deepcopy
    attn = MultiHeadedAttention(h, d_model)
    ff = PositionwiseFeedForward(d_model, d_ff, dropout)
    position = PositionalEncoding(d_model, dropout)
    model = EncoderDecoder(
        Encoder(EncoderLayer(d_model, c(attn), c(ff), dropout), N),
        Decoder(DecoderLayer(d_model, c(attn), c(attn), c(ff), dropout), N),
        nn.Sequential(Embeddings(d_model, src_vocab), c(position)),
        nn.Sequential(Embeddings(d_model, tgt_vocab), c(position)),
        Generator(d_model, tgt_vocab),
    )

    # 初始化模型参数
    for p in model.parameters():
        if p.dim() > 1:
            nn.init.xavier_uniform_(p)
    return model

开始测试

这里进行了10次测试，输入输出词表的大小为11，EncoderLayer和DecoderLayer的层数为2。输入向量经过一次encode之后，又进行了9次的decoder生成，从代码就能看到，decoder传入的是前几步生成的输入，ys向量就是decoder的历史输出。

def inference_test():
    test_model = make_model(11, 11, 2)
    test_model.eval()
    src = torch.LongTensor([[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]])
    src_mask = torch.ones(1, 1, 10)

    memory = test_model.encode(src, src_mask)
    ys = torch.zeros(1, 1).type_as(src)
    breakpoint()

    for i in range(9):
        out = test_model.decode(
            memory, src_mask, ys, subsequent_mask(ys.size(1)).type_as(src.data)
        )
        prob = test_model.generator(out[:, -1])
        _, next_word = torch.max(prob, dim=1)
        next_word = next_word.data[0]
        ys = torch.cat(
            [ys, torch.empty(1, 1).type_as(src.data).fill_(next_word)], dim=1
        )

    print("Example Untrained Model Prediction:", ys)

def run_tests():
    for _ in range(10):
        inference_test()

show_example(run_tests)

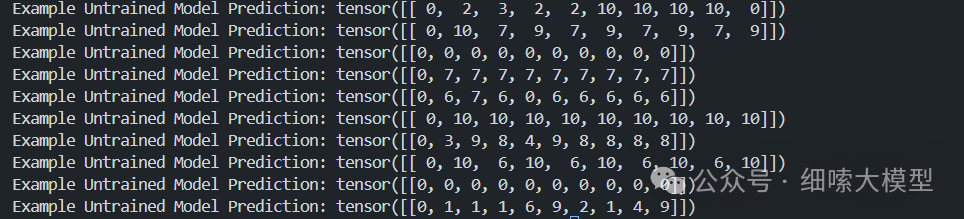
测试结果如图，由于没有训练，所以生成的结果是随机的：

参考文献：

1. The Annotated Transformer (harvard.edu)

2. 理解语言的 Transformer 模型 | TensorFlow Core (google.cn)

3. 第二章：Transformer 模型 · Transformers快速入门

4. The Illustrated Transformer – Jay Alammar – Visualizing machine learning one concept at a time. (jalammar.github.io)

5. 【详细讲解版】史上最全transformer面试题-CSDN博客