注意力与transformer:位置编码与vision transfomer
介绍注意力机制与transfomer模型,特别关注相对位置编码以及一种vision transformer的而变形
个人博客:Sekyoro的博客小屋
个人网站:Proanimer的个人网站
这里介绍一些细节信息.有关位置编码信息和用于图像的transformer.
线性注意力
A t t e n t i o n ( Q , K , V ) = s o f t m a x ( Q K ⊤ ) V Attention(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V})=softmax\left(\boldsymbol{Q}\boldsymbol{K}^\top\right)\boldsymbol{V} Attention(Q,K,V)=softmax(QK⊤)V
其中
Q
∈
R
n
×
d
k
,
K
∈
R
m
×
d
k
,
V
∈
R
m
×
d
v
Q\in\mathbb{R}^{n\times d_k},\boldsymbol{K}\in\mathbb{R}^{m\times d_k},\boldsymbol{V}\in\mathbb{R}^{m\times d_v}
Q∈Rn×dk,K∈Rm×dk,V∈Rm×dv,一般情况下n>d甚至n>>d.所以如果对QKT进行softmax操作,复杂度为O(mn),所以去掉Softmax的Attention的复杂度可以降到最理想的线性级别Linear Attention.
A
t
t
e
n
t
i
o
n
(
Q
,
K
,
V
)
i
=
∑
j
=
1
n
s
i
m
(
q
i
,
k
j
)
v
j
∑
j
=
1
n
s
i
m
(
q
i
,
k
j
)
Attention(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V})_i=\frac{\sum_{j=1}^nsim(\boldsymbol{q}_i,\boldsymbol{k}_j)\boldsymbol{v}_j}{\sum_{j=1}^nsim(\boldsymbol{q}_i,\boldsymbol{k}_j)}
Attention(Q,K,V)i=∑j=1nsim(qi,kj)∑j=1nsim(qi,kj)vj
只要保证Attention相似的分布特性,要求sim(qi,kj)≥0恒成立.比如可以把核函数改为激活函数使得输出大于0.
还可以改成softmax.

其中softmax1、softmax2分别指在第一个(n)、第二个维度(d)进行Softmax运算.
线性Attention的探索:Attention必须有个Softmax吗? - 科学空间|Scientific Spaces提出将指数
eqK泰勒展开, e q i ⊤ k j ≈ 1 + q i ⊤ k j e^{\boldsymbol{q}_i^\top\boldsymbol{k}_j}\approx1+\boldsymbol{q}_i^\top\boldsymbol{k}_j eqi⊤kj≈1+qi⊤kj

此外还有稀疏注意力,这里就不多介绍了.
图像中的transformer与attention
注意力机制以及transformer都是先在NLP领域发展,所以一般attention可能会处理一些1维数据,有CNN与transformer结合的Conformer[2005.08100] Conformer: Convolution-augmented Transformer for Speech Recognition (arxiv.org),conformer中的编码采用相对位置编码.
import torch
import torch.nn.functional as F
from einops import rearrange
from einops.layers.torch import Rearrange
from torch import nn, einsum
def exists(val):
return val is not None
def default(val, d):
return val if exists(val) else d
class Swish(nn.Module):
def forward(self, x):
return x * x.sigmoid()
class FeedForward(nn.Module):
def __init__(self, dim, mult=4, dropout=0.0):
super().__init__()
self.net = nn.Sequential(
nn.Linear(dim, dim * mult),
Swish(), # or can be replace by nn.silu()
nn.Dropout(dropout),
nn.Linear(dim * mult, dim),
nn.Dropout(dropout),
)
def forward(self, x):
return self.net(x)
class Attention(nn.Module):
def __init__(self, dim, heads=8, dim_head=64, dropout=0.0, max_pos_emb=512):
super().__init__()
inner_dim = dim_head * heads
self.heads = heads
self.scale = dim_head**-0.5
self.to_q = nn.Linear(dim, inner_dim, bias=False)
self.to_kv = nn.Linear(dim, inner_dim * 2, bias=False)
self.to_out = nn.Linear(inner_dim, dim)
self.max_pos_emb = max_pos_emb
self.rel_pos_emb = nn.Embedding(2 * max_pos_emb + 1, dim_head)
self.dropout = nn.Dropout(dropout)
def forward(self, x, context=None, mask=None, context_mask=None):
n, device, h, max_pos_emb, has_context = (
x.shape[-2],
x.device,
self.heads,
self.max_pos_emb,
exists(context),
)
context = default(context, x)
q, k, v = (self.to_q(x), *self.to_kv(context).chunk(2, dim=-1))
q, k, v = map(lambda t: rearrange(t, "b n (h d) -> b h n d", h=h), (q, k, v))
dots = einsum("b h i d, b h j d -> b h i j", q, k) * self.scale
# shaw's relative positional embedding
seq = torch.arange(n, device=device)
dist = rearrange(seq, "i -> i ()") - rearrange(seq, "j -> () j")
dist = dist.clamp(-max_pos_emb, max_pos_emb) + max_pos_emb
rel_pos_emb = self.rel_pos_emb(dist).to(q)
pos_attn = einsum("b h n d, n r d -> b h n r", q, rel_pos_emb) * self.scale
dots = dots + pos_attn
if exists(mask) or exists(context_mask):
mask = default(mask, lambda: torch.ones(*x.shape[:2], device=device))
context_mask = (
default(context_mask, mask)
if not has_context
else default(
context_mask, lambda: torch.ones(*context.shape[:2], device=device)
)
)
mask_value = -torch.finfo(dots.dtype).max
mask = rearrange(mask, "b i -> b () i ()") * rearrange(
context_mask, "b j -> b () () j"
)
dots.masked_fill_(~mask, mask_value)
attn = dots.softmax(dim=-1)
out = einsum("b h i j, b h j d -> b h i d", attn, v)
out = rearrange(out, "b h n d -> b n (h d)")
out = self.to_out(out)
return self.dropout(out)
def calc_same_padding(kernel_size):
pad = kernel_size // 2
return pad, pad - (kernel_size + 1) % 2
class DepthWiseConv1d(nn.Module):
def __init__(self, chan_in, chan_out, kernel_size, padding):
super().__init__()
self.padding = padding
self.conv = nn.Conv1d(chan_in, chan_out, kernel_size, groups=chan_in)
def forward(self, x):
x = F.pad(x, self.padding)
return self.conv(x)
class GLU(nn.Module):
def __init__(self, dim):
super().__init__()
self.dim = dim
def forward(self, x):
out, gate = x.chunk(2, dim=self.dim)
return out * gate.sigmoid()
class ConformerConvModule(nn.Module):
def __init__(
self, dim, causal=False, expansion_factor=2, kernel_size=31, dropout=0.0
):
super().__init__()
inner_dim = dim * expansion_factor
padding = calc_same_padding(kernel_size) if not causal else (kernel_size - 1, 0)
self.net = nn.Sequential(
nn.LayerNorm(dim),
Rearrange("b n d -> b d n"),
nn.Conv1d(dim, inner_dim * 2, 1),
GLU(dim=1),
DepthWiseConv1d(
inner_dim, inner_dim, kernel_size=kernel_size, padding=padding
),
nn.BatchNorm1d(inner_dim) if not causal else nn.Identity(),
Swish(),
nn.Conv1d(inner_dim, dim, 1),
Rearrange("b d n -> b n d"),
nn.Dropout(dropout),
)
def forward(self, x):
return self.net(x)
class Scale(nn.Module):
def __init__(self, scale, fn):
super().__init__()
self.scale = scale
self.fn = fn
def forward(self, x, **kwargs):
return self.fn(x, **kwargs) * self.scale
class PreNorm(nn.Module):
def __init__(self, dim, fn):
super().__init__()
self.fn = fn
self.norm = nn.LayerNorm(dim)
def forward(self, x, **kwargs):
x = self.norm(x)
return self.fn(x, **kwargs)
class ConformerBlock(nn.Module):
def __init__(
self,
*,
dim,
dim_head=64,
heads=8,
ff_mult=4,
conv_expansion_factor=2,
conv_kernel_size=31,
attn_dropout=0.0,
ff_dropout=0.0,
conv_dropout=0.0,
conv_causal=False
):
super().__init__()
self.ff1 = FeedForward(dim=dim, mult=ff_mult, dropout=ff_dropout)
self.attn = Attention(
dim=dim, dim_head=dim_head, heads=heads, dropout=attn_dropout
)
self.conv = ConformerConvModule(
dim=dim,
causal=conv_causal,
expansion_factor=conv_expansion_factor,
kernel_size=conv_kernel_size,
dropout=conv_dropout,
)
self.ff2 = FeedForward(dim=dim, mult=ff_mult, dropout=ff_dropout)
self.attn = PreNorm(dim, self.attn)
self.ff1 = Scale(0.5, PreNorm(dim, self.ff1))
self.ff2 = Scale(0.5, PreNorm(dim, self.ff2))
self.post_norm = nn.LayerNorm(dim)
def forward(self, x, mask=None):
x = self.ff1(x) + x
x = self.attn(x, mask=mask) + x
x = self.conv(x) + x
x = self.ff2(x) + x
x = self.post_norm(x)
return x
class Conformer(nn.Module):
def __init__(
self,
dim,
*,
depth,
dim_head=64,
heads=8,
ff_mult=4,
conv_expansion_factor=2,
conv_kernel_size=31,
attn_dropout=0.0,
ff_dropout=0.0,
conv_dropout=0.0,
conv_causal=False
):
super().__init__()
self.dim = dim
self.layers = nn.ModuleList([])
for _ in range(depth):
self.layers.append(
ConformerBlock(
dim=dim,
dim_head=dim_head,
heads=heads,
ff_mult=ff_mult,
conv_expansion_factor=conv_expansion_factor,
conv_kernel_size=conv_kernel_size,
conv_causal=conv_causal,
)
)
def forward(self, x):
for block in self.layers:
x = block(x)
return x
上一节中其实已经充分使用了feature map也就是二维数据上的注意力机制,现在介绍一下在视觉领域表现出色的transformer及其变体.
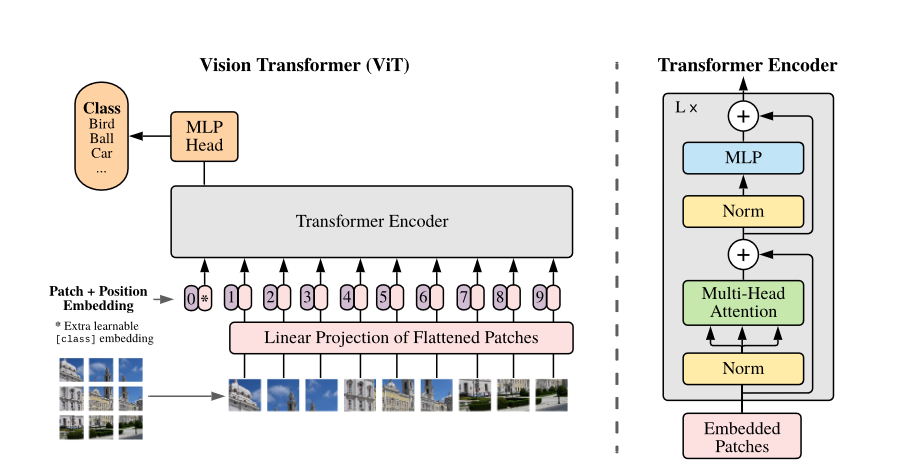
Vision Transformer

将transformer拿到CV领域的出名作品,通过patch embedding得到序列,再加上位置编码就能像在nlp一样处理问题.

import torch
from einops import rearrange
from einops.layers.torch import Rearrange
from torch import nn
# helpers
def pair(t):
return t if isinstance(t, tuple) else (t, t)
def posemb_sincos_2d(h, w, dim, temperature: int = 10000, dtype=torch.float32):
y, x = torch.meshgrid(torch.arange(h), torch.arange(w), indexing="ij")
assert (dim % 4) == 0, "feature dimension must be multiple of 4 for sincos emb"
omega = torch.arange(dim // 4) / (dim // 4 - 1)
omega = 1.0 / (temperature**omega)
y = y.flatten()[:, None] * omega[None, :]
x = x.flatten()[:, None] * omega[None, :]
pe = torch.cat((x.sin(), x.cos(), y.sin(), y.cos()), dim=1)
return pe.type(dtype)
# classes
class FeedForward(nn.Module):
def __init__(self, dim, hidden_dim):
super().__init__()
self.net = nn.Sequential(
nn.LayerNorm(dim),
nn.Linear(dim, hidden_dim),
nn.GELU(),
nn.Linear(hidden_dim, dim),
)
def forward(self, x):
return self.net(x)
class Attention(nn.Module):
def __init__(self, dim, heads=8, dim_head=64):
super().__init__()
inner_dim = dim_head * heads
self.heads = heads
self.scale = dim_head**-0.5
self.norm = nn.LayerNorm(dim)
self.attend = nn.Softmax(dim=-1)
self.to_qkv = nn.Linear(dim, inner_dim * 3, bias=False)
self.to_out = nn.Linear(inner_dim, dim, bias=False)
def forward(self, x):
x = self.norm(x)
qkv = self.to_qkv(x).chunk(3, dim=-1)
q, k, v = map(lambda t: rearrange(t, "b n (h d) -> b h n d", h=self.heads), qkv)
dots = torch.matmul(q, k.transpose(-1, -2)) * self.scale
attn = self.attend(dots)
out = torch.matmul(attn, v)
out = rearrange(out, "b h n d -> b n (h d)")
return self.to_out(out)
class Transformer(nn.Module):
def __init__(self, dim, depth, heads, dim_head, mlp_dim):
super().__init__()
self.norm = nn.LayerNorm(dim)
self.layers = nn.ModuleList([])
for _ in range(depth):
self.layers.append(
nn.ModuleList(
[
Attention(dim, heads=heads, dim_head=dim_head),
FeedForward(dim, mlp_dim),
]
)
)
def forward(self, x):
for attn, ff in self.layers:
x = attn(x) + x
x = ff(x) + x
return self.norm(x)
class SimpleViT(nn.Module):
def __init__(
self,
*,
image_size,
patch_size,
num_classes,
dim,
depth,
heads,
mlp_dim,
channels=3,
dim_head=64
):
super().__init__()
image_height, image_width = pair(image_size)
patch_height, patch_width = pair(patch_size)
assert (
image_height % patch_height == 0 and image_width % patch_width == 0
), "Image dimensions must be divisible by the patch size."
patch_dim = channels * patch_height * patch_width
self.to_patch_embedding = nn.Sequential(
Rearrange(
"b c (h p1) (w p2) -> b (h w) (p1 p2 c)",
p1=patch_height,
p2=patch_width,
),
nn.LayerNorm(patch_dim),
nn.Linear(patch_dim, dim),
nn.LayerNorm(dim),
)
self.pos_embedding = posemb_sincos_2d(
h=image_height // patch_height,
w=image_width // patch_width,
dim=dim,
)
self.transformer = Transformer(dim, depth, heads, dim_head, mlp_dim)
self.pool = "mean"
self.to_latent = nn.Identity()
self.linear_head = nn.Linear(dim, num_classes)
def forward(self, img):
device = img.device
x = self.to_patch_embedding(img)
x += self.pos_embedding.to(device, dtype=x.dtype)
x = self.transformer(x)
x = x.mean(dim=1)
x = self.to_latent(x)
return self.linear_head(x)
上面做了patch之后的位置编码使用三角函数绝对编码,attention和feednetwork与transformer没有什么差别.
卷积注意力
使用vision transformer中使用的绝对位置注意力,但是也可以使用相对位置注意力或者卷积注意力.
卷积位置嵌入( CPE )方法考虑了输入序列的2D性质。采用补零的方式进行2D卷积采集位置信息。卷积位置嵌入( Convolutional Position嵌入,CPE )可用于合并ViT不同阶段的位置数据。CPE可以具体引入到自注意力模块,前馈网络,或者在两个编码器层之间的。
卷积注意力通常方法是利用2D卷积或者depth-wise的卷积将已经做了patch的图像数据进行处理.
class ConvolutionalPositionEmbedding(nn.Module):
def __init__(self, d_model, kernel_size=3, padding=1):
super().__init__()
self.conv = nn.Conv2d(d_model, d_model, kernel_size, padding=padding)
def forward(self, x):
x = x.transpose(1, 2) # 将通道维度和序列长度维度交换
x = x.unsqueeze(2) # 在通道维度和序列长度维度之间添加一个维度
x = self.conv(x) # 对输入进行卷积操作
x = x.squeeze(2) # 移除添加的维度
x = x.transpose(1, 2) # 将通道维度和序列长度维度交换回来
return x
CVT

# #!/usr/bin/env python
# #-*- coding:utf-8 -*-
# Copyleft (C) 2024 proanimer, Inc. All Rights Reserved
# author:proanimer
# createTime:2024/2/18 上午10:38
# lastModifiedTime:2024/2/18 上午10:38
# file:cvt.py
# software: classicNets
#
import torch
import torch.nn as nn
from einops import rearrange, repeat
from einops.layers.torch import Rearrange
from torch import einsum
class SepConv2d(nn.Module):
def __init__(
self,
in_channels,
out_channels,
kernel_size,
stride=1,
padding=0,
dilation=1,
):
super(SepConv2d, self).__init__()
self.depthwise = torch.nn.Conv2d(
in_channels,
in_channels,
kernel_size=kernel_size,
stride=stride,
padding=padding,
dilation=dilation,
groups=in_channels,
)
self.bn = torch.nn.BatchNorm2d(in_channels)
self.pointwise = torch.nn.Conv2d(in_channels, out_channels, kernel_size=1)
def forward(self, x):
x = self.depthwise(x)
x = self.bn(x)
x = self.pointwise(x)
return x
class Residual(nn.Module):
def __init__(self, fn):
super().__init__()
self.fn = fn
def forward(self, x, **kwargs):
return self.fn(x, **kwargs) + x
class PreNorm(nn.Module):
def __init__(self, dim, fn):
super().__init__()
self.norm = nn.LayerNorm(dim)
self.fn = fn
def forward(self, x, **kwargs):
return self.fn(self.norm(x), **kwargs)
class FeedForward(nn.Module):
def __init__(self, dim, hidden_dim, dropout=0.0):
super().__init__()
self.net = nn.Sequential(
nn.Linear(dim, hidden_dim),
nn.GELU(),
nn.Dropout(dropout),
nn.Linear(hidden_dim, dim),
nn.Dropout(dropout),
)
def forward(self, x):
return self.net(x)
class ConvAttention(nn.Module):
def __init__(
self,
dim,
img_size,
heads=8,
dim_head=64,
kernel_size=3,
q_stride=1,
k_stride=1,
v_stride=1,
dropout=0.0,
last_stage=False,
):
super().__init__()
self.last_stage = last_stage
self.img_size = img_size
inner_dim = dim_head * heads
project_out = not (heads == 1 and dim_head == dim)
self.heads = heads
self.scale = dim_head**-0.5
pad = (kernel_size - q_stride) // 2
self.to_q = SepConv2d(dim, inner_dim, kernel_size, q_stride, pad)
self.to_k = SepConv2d(dim, inner_dim, kernel_size, k_stride, pad)
self.to_v = SepConv2d(dim, inner_dim, kernel_size, v_stride, pad)
self.to_out = (
nn.Sequential(nn.Linear(inner_dim, dim), nn.Dropout(dropout))
if project_out
else nn.Identity()
)
def forward(self, x):
b, n, _, h = *x.shape, self.heads
if self.last_stage:
cls_token = x[:, 0]
x = x[:, 1:]
cls_token = rearrange(cls_token.unsqueeze(1), "b n (h d) -> b h n d", h=h)
x = rearrange(x, "b (l w) n -> b n l w", l=self.img_size, w=self.img_size)
q = self.to_q(x)
q = rearrange(q, "b (h d) l w -> b h (l w) d", h=h)
v = self.to_v(x)
v = rearrange(v, "b (h d) l w -> b h (l w) d", h=h)
k = self.to_k(x)
k = rearrange(k, "b (h d) l w -> b h (l w) d", h=h)
if self.last_stage:
q = torch.cat((cls_token, q), dim=2)
v = torch.cat((cls_token, v), dim=2)
k = torch.cat((cls_token, k), dim=2)
dots = einsum("b h i d, b h j d -> b h i j", q, k) * self.scale
attn = dots.softmax(dim=-1)
out = einsum("b h i j, b h j d -> b h i d", attn, v)
out = rearrange(out, "b h n d -> b n (h d)")
out = self.to_out(out)
return out
class Transformer(nn.Module):
def __init__(
self,
dim,
img_size,
depth,
heads,
dim_head,
mlp_dim,
dropout=0.0,
last_stage=False,
):
super().__init__()
self.layers = nn.ModuleList([])
for _ in range(depth):
self.layers.append(
nn.ModuleList(
[
PreNorm(
dim,
ConvAttention(
dim,
img_size,
heads=heads,
dim_head=dim_head,
dropout=dropout,
last_stage=last_stage,
),
),
PreNorm(dim, FeedForward(dim, mlp_dim, dropout=dropout)),
]
)
)
def forward(self, x):
for attn, ff in self.layers:
x = attn(x) + x
x = ff(x) + x
return x
class cvt(nn.Module):
def __init__(
self,
image_size,
in_channels,
num_classes,
dim=64,
kernels=[7, 3, 3],
strides=[4, 2, 2],
heads=[1, 3, 6],
depth=[1, 2, 10],
pool="cls",
dropout=0.0,
emb_dropout=0.0,
scale_dim=4,
):
super(cvt, self).__init__()
assert pool in {
"cls",
"mean",
}, "pool type must be either cls (cls token) or mean (mean pooling)"
self.pool = pool
self.dim = dim
self.stage1_conv_embed = nn.Sequential(
nn.Conv2d(in_channels, dim, kernels[0], strides[0], 2),
Rearrange("b c h w -> b (h w) c", h=image_size // 4, w=image_size // 4),
nn.LayerNorm(dim),
)
self.stage_1_transformer = nn.Sequential(
Transformer(
dim,
img_size=image_size // 4,
depth=depth[0],
heads=heads[0],
dim_head=dim // heads[0],
mlp_dim=dim * scale_dim,
dropout=dropout,
last_stage=True,
),
Rearrange("b (h w) c -> b c h w", h=image_size // 4, w=image_size // 4),
)
# stage 2
in_channels = dim
scale = heads[1] // heads[0]
dim = scale * dim
self.stage2_conv_embed = nn.Sequential(
nn.Conv2d(in_channels, dim, kernels[1], strides[1], 1),
Rearrange("b c h w -> b (h w) c", h=image_size // 8, w=image_size // 8),
nn.LayerNorm(dim),
)
self.stage_2_transformer = nn.Sequential(
Transformer(
dim,
img_size=image_size // 8,
depth=depth[1],
heads=heads[1],
dim_head=dim // heads[1],
mlp_dim=dim * scale_dim,
dropout=dropout,
last_stage=True,
),
Rearrange("b (h w) c -> b c h w", h=image_size // 8, w=image_size // 8),
)
# stage 3
in_channels = dim
scale = heads[2] // heads[1]
dim = scale * dim
self.stage3_conv_embed = nn.Sequential(
nn.Conv2d(in_channels, dim, kernels[2], strides[2], 1),
Rearrange("b c h w -> b (h w) c", h=image_size // 16, w=image_size // 16),
nn.LayerNorm(dim),
)
self.stage_3_transformer = nn.Sequential(
Transformer(
dim=dim,
img_size=image_size // 16,
depth=depth[2],
heads=heads[2],
dim_head=self.dim,
mlp_dim=dim * scale_dim,
dropout=dropout,
last_stage=True,
),
)
self.cls_token = nn.Parameter(torch.randn(1, 1, dim))
self.drop_large = nn.Dropout(emb_dropout)
self.mlp_head = nn.Sequential(nn.LayerNorm(dim), nn.Linear(dim, num_classes))
def forward(self,img):
xs = self.stage1_conv_embed(img)
xs = self.stage1_transformer(xs)
xs = self.stage2_conv_embed(xs)
xs = self.stage2_transformer(xs)
xs = self.stage3_conv_embed(xs)
b, n, _ = xs.shape
cls_tokens = repeat(self.cls_token, '() n d -> b n d', b=b)
xs = torch.cat((cls_tokens, xs), dim=1)
xs = self.stage3_transformer(xs)
xs = xs.mean(dim=1) if self.pool == 'mean' else xs[:, 0]
xs = self.mlp_head(xs)
return xs
PVT

# #!/usr/bin/env python
# #-*- coding:utf-8 -*-
# Copyleft (C) 2024 proanimer, Inc. All Rights Reserved
# author:proanimer
# createTime:2024/2/18 下午2:22
# lastModifiedTime:2024/2/18 下午2:22
# file:pvt.py
# software: classicNets
#
from functools import partial
import torch
import torch.nn as nn
import torch.nn.functional as F
from timm.models.layers import DropPath, to_2tuple, trunc_normal_
class Mlp(nn.Module):
def __init__(
self,
in_features,
hidden_features=None,
out_features=None,
act_layer=nn.GELU,
drop=0.0,
):
super().__init__()
out_features = out_features or in_features
hidden_features = hidden_features or in_features
self.fc1 = nn.Linear(in_features, hidden_features)
self.act = act_layer()
self.fc2 = nn.Linear(hidden_features, out_features)
self.drop = nn.Dropout(drop)
def forward(self, x):
x = self.fc1(x)
x = self.act(x)
x = self.drop(x)
x = self.fc2(x)
x = self.drop(x)
return x
class Attention(nn.Module):
def __init__(
self,
dim,
num_heads=8,
qkv_bias=False,
qk_scale=None,
attn_drop=0.0,
proj_drop=0.0,
sr_ratio=1,
):
super().__init__()
assert (
dim % num_heads == 0
), f"dim {dim} should be divided by num_heads {num_heads}."
self.dim = dim
self.num_heads = num_heads
head_dim = dim // num_heads
self.scale = qk_scale or head_dim**-0.5
self.q = nn.Linear(dim, dim, bias=qkv_bias)
self.kv = nn.Linear(dim, dim * 2, bias=qkv_bias)
self.attn_drop = nn.Dropout(attn_drop)
self.proj = nn.Linear(dim, dim)
self.proj_drop = nn.Dropout(proj_drop)
self.sr_ratio = sr_ratio
if sr_ratio > 1:
self.sr = nn.Conv2d(dim, dim, kernel_size=sr_ratio, stride=sr_ratio)
self.norm = nn.LayerNorm(dim)
def forward(self, x, H, W):
B, N, C = x.shape
q = (
self.q(x)
.reshape(B, N, self.num_heads, C // self.num_heads)
.permute(0, 2, 1, 3)
)
if self.sr_ratio > 1:
x_ = x.permute(0, 2, 1).reshape(B, C, H, W)
x_ = self.sr(x_).reshape(B, C, -1).permute(0, 2, 1)
x_ = self.norm(x_)
kv = (
self.kv(x_)
.reshape(B, -1, 2, self.num_heads, C // self.num_heads)
.permute(2, 0, 3, 1, 4)
)
else:
kv = (
self.kv(x)
.reshape(B, -1, 2, self.num_heads, C // self.num_heads)
.permute(2, 0, 3, 1, 4)
)
k, v = kv[0], kv[1]
attn = (q @ k.transpose(-2, -1)) * self.scale # q (B,H,N,C) K(B,H,C,N)
attn = attn.softmax(dim=-1)
attn = self.attn_drop(attn)
x = (
(attn @ v).transpose(1, 2).reshape(B, N, C)
) # (B,H,N,N) @ (B,H,N,C) -> (B,H,N,C)
x = self.proj(x)
x = self.proj_drop(x)
return x
class Block(nn.Module):
def __init__(
self,
dim,
num_heads,
mlp_ratio=4.0,
qkv_bias=False,
qk_scale=None,
drop=0.0,
attn_drop=0.0,
drop_path=0.0,
act_layer=nn.GELU,
norm_layer=nn.LayerNorm,
sr_ratio=1,
):
super().__init__()
self.norm1 = norm_layer(dim)
self.attn = Attention(
dim,
num_heads=num_heads,
qkv_bias=qkv_bias,
qk_scale=qk_scale,
attn_drop=attn_drop,
proj_drop=drop,
sr_ratio=sr_ratio,
)
# NOTE: drop path for stochastic depth, we shall see if this is better than dropout here
self.drop_path = DropPath(drop_path) if drop_path > 0.0 else nn.Identity()
self.norm2 = norm_layer(dim)
mlp_hidden_dim = int(dim * mlp_ratio)
self.mlp = Mlp(
in_features=dim,
hidden_features=mlp_hidden_dim,
act_layer=act_layer,
drop=drop,
)
def forward(self, x, H, W):
x = x + self.drop_path(self.attn(self.norm1(x), H, W))
x = x + self.drop_path(self.mlp(self.norm2(x)))
return x
class PatchEmbed(nn.Module):
"""Image to Patch Embedding"""
def __init__(self, img_size=224, patch_size=16, in_chans=3, embed_dim=768):
super().__init__()
img_size = to_2tuple(img_size)
patch_size = to_2tuple(patch_size)
self.img_size = img_size
self.patch_size = patch_size
assert (
img_size[0] % patch_size[0] == 0 and img_size[1] % patch_size[1] == 0
), f"img_size {img_size} should be divided by patch_size {patch_size}."
self.H, self.W = img_size[0] // patch_size[0], img_size[1] // patch_size[1]
self.num_patches = self.H * self.W
self.proj = nn.Conv2d(
in_chans, embed_dim, kernel_size=patch_size, stride=patch_size
)
self.norm = nn.LayerNorm(embed_dim)
def forward(self, x):
B, C, H, W = x.shape
x = (
self.proj(x).flatten(2).transpose(1, 2)
) # B,C,H,W->B,embed_dim,seq*seq->B,seq*seq,embed_dim
x = self.norm(x)
H, W = H // self.patch_size[0], W // self.patch_size[1]
return x, (H, W)
class PyramidVisionTransformer(nn.Module):
def __init__(
self,
img_size=224,
patch_size=16,
in_chans=3,
num_classes=1000,
embed_dims=[64, 128, 256, 512],
num_heads=[1, 2, 4, 8],
mlp_ratios=[4, 4, 4, 4],
qkv_bias=False,
qk_scale=None,
drop_rate=0.0,
attn_drop_rate=0.0,
drop_path_rate=0.0,
norm_layer=nn.LayerNorm,
depths=[3, 4, 6, 3],
sr_ratios=[8, 4, 2, 1],
F4=False,
num_stages=4,
):
super().__init__()
self.depths = depths
self.F4 = F4
self.num_stages = num_stages
dpr = [
x.item() for x in torch.linspace(0, drop_path_rate, sum(depths))
] # stochastic depth decay rule
cur = 0
for i in range(num_stages):
patch_embed = PatchEmbed(
img_size=img_size if i == 0 else img_size // (2 ** (i + 1)),
patch_size=patch_size if i == 0 else 2,
in_chans=in_chans if i == 0 else embed_dims[i - 1],
embed_dim=embed_dims[i],
) # [B,seq=num_patches,dim=patch_size**2*embed_dim]
num_patches = (
patch_embed.num_patches
if i != num_stages - 1
else patch_embed.num_patches + 1
)
pos_embed = nn.Parameter(torch.zeros(1, num_patches, embed_dims[i]))
pos_drop = nn.Dropout(p=drop_rate)
block = nn.ModuleList(
[
Block(
dim=embed_dims[i],
num_heads=num_heads[i],
mlp_ratio=mlp_ratios[i],
qkv_bias=qkv_bias,
qk_scale=qk_scale,
drop=drop_rate,
attn_drop=attn_drop_rate,
drop_path=dpr[cur + j],
norm_layer=norm_layer,
sr_ratio=sr_ratios[i],
)
for j in range(depths[i])
]
)
cur += depths[i]
setattr(self, f"patch_embed{i + 1}", patch_embed)
setattr(self, f"pos_embed{i + 1}", pos_embed)
setattr(self, f"pos_drop{i + 1}", pos_drop)
setattr(self, f"block{i + 1}", block)
trunc_normal_(pos_embed, std=0.02)
# init weights
self.apply(self._init_weights)
# self.init_weights(pretrained)
def _init_weights(self, m):
if isinstance(m, nn.Linear):
trunc_normal_(m.weight, std=0.02)
if isinstance(m, nn.Linear) and m.bias is not None:
nn.init.constant_(m.bias, 0)
elif isinstance(m, nn.LayerNorm):
nn.init.constant_(m.bias, 0)
nn.init.constant_(m.weight, 1.0)
def _get_pos_embed(self, pos_embed, patch_embed, H, W):
if H * W == self.patch_embed1.num_patches:
return pos_embed
else:
return (
F.interpolate(
pos_embed.reshape(1, patch_embed.H, patch_embed.W, -1).permute(
0, 3, 1, 2
),
size=(H, W),
mode="bilinear",
)
.reshape(1, -1, H * W)
.permute(0, 2, 1)
)
def forward_features(self, x):
outs = []
B = x.shape[0]
for i in range(self.num_stages):
patch_embed = getattr(self, f"patch_embed{i + 1}")
pos_embed = getattr(self, f"pos_embed{i + 1}")
pos_drop = getattr(self, f"pos_drop{i + 1}")
block = getattr(self, f"block{i + 1}")
x, (H, W) = patch_embed(x)
if i == self.num_stages - 1:
pos_embed = self._get_pos_embed(pos_embed[:, 1:], patch_embed, H, W)
else:
pos_embed = self._get_pos_embed(pos_embed, patch_embed, H, W)
x = pos_drop(x + pos_embed)
for blk in block:
x = blk(x, H, W)
x = x.reshape(B, H, W, -1).permute(0, 3, 1, 2).contiguous()
outs.append(x)
return outs
def forward(self, x):
x = self.forward_features(x)
if self.F4:
x = x[3:4]
return x
CPVT中的PEG

conditional position encoding

出自论文2102.10882.pdf (arxiv.org)
import torch
import torch.nn as nn
class PEG(nn.Module):
def __init__(self, dim=256, k=3):
self.proj = nn.Conv2d(dim, dim, k, 1, k//2, groups=dim)
# Only for demo use, more complicated functions are effective too.
def forward(self, x, H, W):
B, N, C = x.shape
cls_token, feat_token = x[:, 0], x[:, 1:] # cls token不参与PEG
cnn_feat = feat_token.transpose(1, 2).view(B, C, H, W)
x = self.proj(cnn_feat) + cnn_feat # 产生PE加上自身
x = x.flatten(2).transpose(1, 2)
x = torch.cat((cls_token.unsqueeze(1), x), dim=1)
return x
class VisionTransformer:
def __init__(layers=12, dim=192, nhead=3, img_size=224, patch_size=16):
self.pos_block = PEG(dim)
self.blocks = nn.ModuleList([TransformerEncoderLayer(dim
, nhead, dim*4) for _ in range(layers)])
self.patch_embed = PatchEmbed(img_size, patch_size, dim
*4)
def forward_features(self, x):
B, C, H, W = x.shape
x, patch_size = self.patch_embed(x)
_H, _W = H // patch_size, W // patch_size
x = torch.cat((self.cls_tokens, x), dim=1)
for i, blk in enumerate(self.blocks):
x = blk(x)
if i == 0: # 第一个encoder之后施加PEG
x = self.pos_block(x, _H, _W)
return x[:, 0]
LocalVit

class Transformer(nn.Module):
def __init__(self, dim, depth, heads, dim_head, patch_height, patch_width, scale = 4, depth_kernel = 3, dropout = 0.):
super().__init__()
self.layers = nn.ModuleList([])
for _ in range(depth):
self.layers.append(nn.ModuleList([
Residual(PreNorm(dim, Attention(dim, heads = heads, dim_head = dim_head, dropout = dropout))),
Residual(PreNorm(dim, ConvFF(dim, scale, depth_kernel, patch_height, patch_width)))
]))
def forward(self, x):
for attn, convff in self.layers:
x = attn(x)
cls_tokens = x[:, 0]
x = convff(x[:, 1:])
x = torch.cat((cls_tokens.unsqueeze(1), x), dim=1)
return xclass ConvFF(nn.Module):
def __init__(self, dim = 192, scale = 4, depth_kernel = 3, patch_height = 14, patch_width = 14, dropout=0.):
super().__init__()
scale_dim = dim*scale
self.up_proj = nn.Sequential(
Rearrange('b (h w) c -> b c h w', h=patch_height, w=patch_width),
nn.Conv2d(dim, scale_dim, kernel_size=1),
nn.Hardswish()
)
self.depth_conv = nn.Sequential(
nn.Conv2d(scale_dim, scale_dim, kernel_size=depth_kernel, padding=1, groups=scale_dim, bias=True),
nn.Conv2d(scale_dim, scale_dim, kernel_size=1, bias=True),
nn.Hardswish()
)
self.down_proj = nn.Sequential(
nn.Conv2d(scale_dim, dim, kernel_size=1),
nn.Dropout(dropout),
Rearrange('b c h w ->b (h w) c')
)
在feed-forward中使用2d的卷积.
transformer中的绝对和相对位置编码
位置编码可以分为使用nn.Embedding或者nn.Parameter的可学习参数,也可以直接使用固定的值,比如三角函数编码.此外可以分为相对位置和绝对位置编码
绝对位置编码
transformer中使用了位置编码信息,被认为是绝对位置编码
class PositionalEncoding(nn.Module):
"Implement the PE function."
def __init__(self, d_model, dropout, max_len=5000):
super(PositionalEncoding, self).__init__()
self.dropout = nn.Dropout(p=dropout)
# Compute the positional encodings once in log space.
pe = torch.zeros(max_len, d_model)
position = torch.arange(0, max_len).unsqueeze(1)
div_term = torch.exp(torch.arange(0, d_model, 2) *
-(math.log(10000.0) / d_model))
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
pe = pe.unsqueeze(0)
self.register_buffer('pe', pe)
def forward(self, x):
x = x + Variable(self.pe[:, :x.size(1)],
requires_grad=False)
return self.dropout(x)
我们可能希望使用相对位置编码而不是绝对位置编码,原因有很多。首先,使用绝对位置信息必然意味着模型可以处理的token数量有限制。假设一个语言模型最多只能编码1024个位置。这必然意味着任何长于1024个token的序列都不能被模型处理;相对位置编码可以推广到看不见长度的序列,因为理论上它编码的唯一信息是两个标记之间的相对成对距离。
相对位置编码的历史
相对位置嵌入( Relative Position Embedding,RPE )技术主要用于将与相对位置相关的信息纳入到注意力模块中。该技术基于这样的思想:块之间的空间关系比它们的绝对位置承载更多的权重。为了计算RPE值,使用了基于可学习参数的查找表。查找过程由图像patch间的相对距离决定。虽然RPE技术可以扩展到不同长度的序列,但它可能会增加训练和测试时间。
在attention is all you need中的attention中,自我注意力可以表述为如下,并使用三角函数索引进行位置编码.
z
i
=
∑
j
=
1
n
α
i
j
(
x
j
W
V
)
α
i
j
=
exp
e
i
j
∑
k
=
1
n
exp
e
i
k
e
i
j
=
(
x
i
W
Q
)
(
x
j
W
K
)
T
d
z
z_i=\sum_{j=1}^n\alpha_{ij}(x_jW^V) \\ \alpha_{ij}=\frac{\exp e_{ij}}{\sum_{k=1}^n\exp e_{ik}} \\ e_{ij}=\frac{(x_iW^Q)(x_jW^K)^T}{\sqrt{d_z}}
zi=j=1∑nαij(xjWV)αij=∑k=1nexpeikexpeijeij=dz(xiWQ)(xjWK)T
1D数据
Shaw
相对位置编码在swin-transformer以及Self-Attention with Relative Position Representations中都有体现.较早的论文1803.02155.pdf (arxiv.org)
z
i
=
∑
j
=
1
n
α
i
j
(
x
j
W
V
+
a
i
j
V
)
e
i
j
=
x
i
W
Q
(
x
j
W
K
+
a
i
j
K
)
T
d
z
a
i
j
K
=
w
c
l
i
p
(
j
−
i
,
k
)
K
a
i
j
V
=
w
c
l
i
p
(
j
−
i
,
k
)
V
clip
(
x
,
k
)
=
max
(
−
k
,
min
(
k
,
x
)
)
z_i=\sum_{j=1}^n\alpha_{ij}(x_jW^V+a_{ij}^V) \\ e_{ij}=\frac{x_iW^Q(x_jW^K+a_{ij}^K)^T}{\sqrt{d_z}} \\ \begin{aligned} a_{ij}^{K}& =w_{\mathrm{clip}(j-i,k)}^{K} \\ a_{ij}^{V}& =w_{\mathrm{clip}(j-i,k)}^{V} \\ \operatorname{clip}(x,k)& =\max(-k,\min(k,x)) \end{aligned}
zi=j=1∑nαij(xjWV+aijV)eij=dzxiWQ(xjWK+aijK)TaijKaijVclip(x,k)=wclip(j−i,k)K=wclip(j−i,k)V=max(−k,min(k,x))
其中的wk和wv是需要训练的参数.
w
K
=
(
w
−
k
K
,
…
,
w
k
K
)
w
V
=
(
w
−
k
V
˙
,
…
,
w
k
V
)
w^{K}=(w_{-k}^{K},\ldots,w_{k}^{K}) \\ w^{V}=(\dot{w_{-k}^{V}},\ldots,w_{k}^{V})
wK=(w−kK,…,wkK)wV=(w−kV˙,…,wkV)
以下是1803.02155.pdf (arxiv.org)中的相对位置注意力


# shaw's relative positional embedding
seq = torch.arange(n, device=device)
dist = rearrange(seq, "i -> i ()") - rearrange(seq, "j -> () j")
dist = dist.clamp(-max_pos_emb, max_pos_emb) + max_pos_emb
rel_pos_emb = self.rel_pos_emb(dist).to(q)
pos_attn = einsum("b h n d, n r d -> b h n r", q, rel_pos_emb) * self.scale
dots = dots + pos_attn
if exists(mask) or exists(context_mask):
mask = default(mask, lambda: torch.ones(*x.shape[:2], device=device))
context_mask = (
default(context_mask, mask)
if not has_context
else default(
context_mask, lambda: torch.ones(*context.shape[:2], device=device)
)
)
mask_value = -torch.finfo(dots.dtype).max
mask = rearrange(mask, "b i -> b () i ()") * rearrange(
context_mask, "b j -> b () () j"
)
dots.masked_fill_(~mask, mask_value)
attn = dots.softmax(dim=-1)
out = einsum("b h i j, b h j d -> b h i d", attn, v)
out = rearrange(out, "b h n d -> b n (h d)")
out = self.to_out(out)
transformer-xl
众所周知,q=xWQ,k=xWK,加入相对位置编码后,展开一般注意力公式有


Transformer-XL的做法很简单,直接将 p j p_j pj 替换为相对位置向量 R i − j R_{i-j} Ri−j, 至于两个 p i p_i pi , 则干脆替换为两个可训练的问量 u , v u,v u,v
之后的改进也是基于此,并且不再改动计算V了.
在transformer-xl(或者也是XLNET中使用的编码)中
e
i
j
=
(
x
i
W
Q
+
u
)
(
x
j
W
K
)
T
+
(
x
i
W
Q
+
v
)
(
s
i
−
j
W
R
)
T
d
z
,
e_{ij}=\frac{(\mathbf{x}_i\mathbf{W}^Q+\mathbf{u})(\mathbf{x}_j\mathbf{W}^K)^T+(\mathbf{x}_i\mathbf{W}^Q+\mathbf{v})(\mathbf{s}_{i-j}\mathbf{W}^R)^T}{\sqrt{d_z}},
eij=dz(xiWQ+u)(xjWK)T+(xiWQ+v)(si−jWR)T,
class PositionalEmbedding(nn.Module):
def __init__(self, demb):
super(PositionalEmbedding, self).__init__()
self.demb = demb
inv_freq = 1 / (10000 ** (torch.arange(0.0, demb, 2.0) / demb))
def forward(self, pos_seq):
sinusoid_inp = torch.outer(pos_seq, self.inv_freq) # 向量之间相乘
pos_emb = torch.cat([sinusoid_inp.sin(), sinusoid_inp.cos()], dim=-1)
return pos_emb[:,None,:]
w_head_q = w_head_q.view(qlen, bsz, self.n_head, self.d_head) # qlen x bsz x n_head x d_head
w_head_k = w_head_k.view(klen, bsz, self.n_head, self.d_head) # qlen x bsz x n_head x d_head
w_head_v = w_head_v.view(klen, bsz, self.n_head, self.d_head) # qlen x bsz x n_head x d_head
r_head_k = r_head_k.view(rlen, self.n_head, self.d_head) # qlen x n_head x d_head
#### compute attention score
rw_head_q = w_head_q + r_w_bias #加上biase # qlen x bsz x n_head x d_head
AC = torch.einsum('ibnd,jbnd->ijbn', (rw_head_q, w_head_k)) # qlen x klen x bsz x n_head
rr_head_q = w_head_q + r_r_bias #加上biase
BD = torch.einsum('ibnd,jnd->ijbn', (rr_head_q, r_head_k)) # qlen x klen x bsz x n_head
BD = self._rel_shift(BD)
# [qlen x klen x bsz x n_head]
attn_score = AC + BD
attn_score.mul_(self.scale)
其中u,v是两个可学习参数,WR是一个矩阵将si-j投影到一个与位置相关的key向量.
Music transformer
后来Huang对shaw的相对位置编码进行改进

Huang
此外还有2009.13658.pdf (arxiv.org)提出的
e
i
j
=
(
x
i
W
Q
+
p
i
j
)
(
x
j
W
K
+
p
i
j
)
T
−
p
i
j
p
i
j
T
d
z
,
e_{ij}=\frac{(\mathbf{x}_i\mathbf{W}^Q+\mathbf{p}_{ij})(\mathbf{x}_j\mathbf{W}^K+\mathbf{p}_{ij})^T-\mathbf{p}_{ij}\mathbf{p}_{ij}^T}{\sqrt{d_z}},
eij=dz(xiWQ+pij)(xjWK+pij)T−pijpijT,
T5

DeBERTa

总结下来就是在计算attention权重时或者在计算最后的注意力时加上一个与相对位置信息相关的值.这个值的计算通常类似如下
# shaw's relative positional embedding
seq = torch.arange(n, device=device)
dist = rearrange(seq, "i -> i ()") - rearrange(seq, "j -> () j")
dist = dist.clamp(-max_pos_emb, max_pos_emb) + max_pos_emb
rel_pos_emb = self.rel_pos_emb(dist).to(q)
以上大多用于1D数据比如音频和文字.
2D数据
Stand-Alone Self-Attention in Vision Models

公式如下
y
i
j
=
∑
a
,
b
∈
N
k
(
i
,
j
)
softmax
a
b
(
q
i
j
⊤
k
a
b
+
q
i
j
⊤
r
a
−
i
,
b
−
j
)
v
a
b
y_{ij}=\sum_{a,b\in\mathcal{N}_{k}(i,j)}\text{softmax}_{ab}\left(q_{ij}^{\top}k_{ab}+q_{ij}^{\top}r_{a-i,b-j}\right)v_{ab}
yij=a,b∈Nk(i,j)∑softmaxab(qij⊤kab+qij⊤ra−i,b−j)vab
对相对距离进行维度分解,每个元素ab∈Nk(i,j)得到两个距离:行偏移量a-i和列偏移量b-j .
行偏移和列偏移分别与一个嵌入ra-i和rb-j相关联,每个嵌入维度为1/2dout,行偏移嵌入和列偏移嵌入被串联起来形成ra-i,b-j。
或者表示如下
e
i
j
=
(
x
i
W
Q
)
(
x
j
W
K
+
c
o
n
c
a
t
(
p
δ
x
ˉ
K
,
p
δ
y
ˉ
K
)
)
T
d
z
,
e_{ij}=\frac{(\mathbf{x}_i\mathbf{W}^Q)(\mathbf{x}_j\mathbf{W}^K+concat(\mathbf{p}_{\delta\bar{x}}^K,\mathbf{p}_{\delta\bar{y}}^K))^T}{\sqrt{d_z}},
eij=dz(xiWQ)(xjWK+concat(pδxˉK,pδyˉK))T,
其中p是可训练参数,长度是1/2dz

import torch
import torch.nn as nn
import torch.nn.functional as F
use_cuda = torch.cuda.is_available()
device = torch.device("cuda" if use_cuda else "cpu")
class SASA_Layer(nn.Module):
def __init__(self, in_channels, kernel_size=7, num_heads=8, image_size=224, inference=False):
super(SASA_Layer, self).__init__()
self.kernel_size = min(kernel_size, image_size) # receptive field shouldn't be larger than input H/W
self.num_heads = num_heads
self.dk = self.dv = in_channels
self.dkh = self.dk // self.num_heads
self.dvh = self.dv // self.num_heads
assert self.dk % self.num_heads == 0, "dk should be divided by num_heads. (example: dk: 32, num_heads: 8)"
assert self.dk % self.num_heads == 0, "dv should be divided by num_heads. (example: dv: 32, num_heads: 8)"
self.k_conv = nn.Conv2d(self.dk, self.dk, kernel_size=1).to(device)
self.q_conv = nn.Conv2d(self.dk, self.dk, kernel_size=1).to(device)
self.v_conv = nn.Conv2d(self.dv, self.dv, kernel_size=1).to(device)
# Positional encodings
self.rel_encoding_h = nn.Parameter(torch.randn(self.dk // 2, self.kernel_size, 1), requires_grad=True)
self.rel_encoding_w = nn.Parameter(torch.randn(self.dk // 2, 1, self.kernel_size), requires_grad=True)
# later access attention weights
self.inference = inference
if self.inference:
self.register_parameter('weights', None)
def forward(self, x):
batch_size, _, height, width = x.size()
# Compute k, q, v
padded_x = F.pad(x, [(self.kernel_size-1)//2, (self.kernel_size-1)-((self.kernel_size-1)//2), (self.kernel_size-1)//2, (self.kernel_size-1)-((self.kernel_size-1)//2)])
k = self.k_conv(padded_x)
q = self.q_conv(x)
v = self.v_conv(padded_x)
# Unfold patches into [BS, num_heads*depth, horizontal_patches, vertical_patches, kernel_size, kernel_size]
k = k.unfold(2, self.kernel_size, 1).unfold(3, self.kernel_size, 1)
v = v.unfold(2, self.kernel_size, 1).unfold(3, self.kernel_size, 1)
# Reshape into [BS, num_heads, horizontal_patches, vertical_patches, depth_per_head, kernel_size*kernel_size]
k = k.reshape(batch_size, self.num_heads, height, width, self.dkh, -1)
v = v.reshape(batch_size, self.num_heads, height, width, self.dvh, -1)
# Reshape into [BS, num_heads, height, width, depth_per_head, 1]
q = q.reshape(batch_size, self.num_heads, height, width, self.dkh, 1)
qk = torch.matmul(q.transpose(4, 5), k)
qk = qk.reshape(batch_size, self.num_heads, height, width, self.kernel_size, self.kernel_size)
# Add positional encoding
qr_h = torch.einsum('bhxydz,cij->bhxyij', q, self.rel_encoding_h)
qr_w = torch.einsum('bhxydz,cij->bhxyij', q, self.rel_encoding_w)
qk += qr_h
qk += qr_w
qk = qk.reshape(batch_size, self.num_heads, height, width, 1, self.kernel_size*self.kernel_size)
weights = F.softmax(qk, dim=-1)
if self.inference:
self.weights = nn.Parameter(weights)
attn_out = torch.matmul(weights, v.transpose(4, 5))
attn_out = attn_out.reshape(batch_size, -1, height, width)
return attn_out
上面的代码可能有些问题,应该是将i,j的距离差嵌入到一个embedding中更合适
Rethinking and Improving Relative Position Encoding for Vision Transformer
这是篇好文章,关于注意力中相对位置用于2d图像数据的方法.也是在上面SASA的一种改进.

以往的相对位置编码方法都依赖于输入嵌入。这就带来了一个问题,即编码能否独立于输入?
论文引入相对位置编码的偏向模式和语境模式来研究该问题。前者独立于输入嵌入,而后者考虑了与查询、键或值的交互。也就上图的两种模式.
e
i
j
=
(
x
i
W
Q
)
(
x
j
W
K
)
T
+
b
i
j
d
z
b
i
j
=
r
i
j
f
o
r
b
i
a
s
m
o
d
e
b
i
j
=
(
x
i
W
Q
)
r
i
j
f
o
r
c
o
n
t
e
x
t
m
o
d
e
e_{ij}=\frac{(\mathbf{x}_i\mathbf{W}^Q)(\mathbf{x}_j\mathbf{W}^K)^T\color{blue}{+}b_{ij}}{\sqrt{d_z}} \\ b_{ij}=\bold{r}_{ij} \space for \space bias \space mode\\ b_{ij}=(x_{i}W^Q)r_{ij}\space for\space context \space mode\\
eij=dz(xiWQ)(xjWK)T+bijbij=rij for bias modebij=(xiWQ)rij for context mode
计算attention weight加上一个偏置,在bias模式下,这个偏置是一个可学习的参数,表示相对位置的权重.
在context模式下,有多种可行的方式.其中r是一个可训练的向量,也表示相对位置,但它会与Q或K交互.
b
i
j
=
(
x
i
W
Q
)
(
r
i
j
K
)
T
+
(
x
j
W
K
)
(
r
i
j
Q
)
T
b_{ij}=(\mathbf{x}_i\mathbf{W}^Q)(\mathbf{r}_{ij}^K)^T+(\mathbf{x}_j\mathbf{W}^K)(\mathbf{r}_{ij}^Q)^T
bij=(xiWQ)(rijK)T+(xjWK)(rijQ)T
此外context模式也可以应用于value嵌入
z
i
=
∑
j
=
1
n
α
i
j
(
x
j
W
V
+
r
i
j
V
)
,
\mathbf{z}_i=\sum_{j=1}^n\alpha_{ij}(\mathbf{x}_j\mathbf{W}^V\color{red}{+}\mathbf{r}_{ij}^V),
zi=j=1∑nαij(xjWV+rijV),
为了计算二维图像平面上的相对位置并定义相对权重rij,提出了两种无向映射方法Euclidean和Quantization,以及两种有向映射方法Cross和Product。
r
i
j
=
p
I
(
i
,
j
)
,
\mathbf{r}_{ij}=\mathbf{p}_{I(i,j)},
rij=pI(i,j),
I ( i , j ) = g ( ( x ~ i − x ~ j ) 2 + ( y ~ i − y ~ j ) 2 ) , I(i,j)=g(\sqrt{(\tilde{x}_i-\tilde{x}_j)^2+(\tilde{y}_i-\tilde{y}_j)^2}), I(i,j)=g((x~i−x~j)2+(y~i−y~j)2),
在上述欧几里得方法中,距离较近的两个具有不同相对距离的邻居可能被映射到同一个索引中,例如二维相对位置( 1、0 )和( 1 , 1)都被映射到索引1中。假设近邻应该是分离的。因此对欧氏距离进行量化,即将不同的实数映射成不同的整数。
I
(
i
,
j
)
=
g
(
q
u
a
n
t
(
(
x
~
i
−
x
~
j
)
2
+
(
y
~
i
−
y
~
j
)
2
)
.
I(i,j)=g(quant(\sqrt{(\tilde{x}_i-\tilde{x}_j)^2+(\tilde{y}_i-\tilde{y}_j)^2}).
I(i,j)=g(quant((x~i−x~j)2+(y~i−y~j)2).
运算quant ( · )将一组实数{ 0,1,1.41,2,2.24,… }映射为一组整数{ 0,1,2,3,4,… } .这种方法也是无向的.
像素的位置方向对图像也很重要,因此提出了有向映射方法。这种方法被称为Cross方法,它分别在水平和垂直方向上计算编码,然后进行汇总。方法如下
r
i
j
=
p
I
x
~
(
i
,
j
)
x
~
+
p
I
y
~
(
i
,
j
)
y
~
,
I
x
~
(
i
,
j
)
=
g
(
x
i
~
−
x
j
~
)
,
I
y
~
(
i
,
j
)
=
g
(
y
~
i
−
y
~
j
)
,
\begin{gathered} \mathbf{r}_{ij}=\mathbf{p}_{I^{\tilde{x}}(i,j)}^{\tilde{x}}+\mathbf{p}_{I^{\tilde{y}}(i,j)}^{\tilde{y}}, \\ I^{\tilde{x}}(i,j)=g(\tilde{x_{i}}-\tilde{x_{j}}), \\ I^{\tilde{y}}(i,j)=g(\tilde{y}_i-\tilde{y}_j), \end{gathered}
rij=pIx~(i,j)x~+pIy~(i,j)y~,Ix~(i,j)=g(xi~−xj~),Iy~(i,j)=g(y~i−y~j),
如果某个方向上的距离是相同的,那么Cross方法将不同的相对位置编码到同一个嵌入中,此外带来了额外的计算开销。为了提高效率并包含更多的方向性信息,设计了Product方法,公式如下:

其他
Swin transformer
[2103.14030] Swin Transformer: Hierarchical Vision Transformer using Shifted Windows (arxiv.org)
[2111.09883] Swin Transformer V2: Scaling Up Capacity and Resolution (arxiv.org)

Ω
(
M
S
A
)
=
4
h
w
C
2
+
2
(
h
w
)
2
C
,
Ω
(
W
−
M
S
A
)
=
4
h
w
C
2
+
2
M
2
h
w
C
,
\begin{aligned}\Omega(\mathbf{MSA})&=4hwC^2+2(hw)^2C,\\\Omega(\mathbf{W-MSA})&=4hwC^2+2M^2hwC,\end{aligned}
Ω(MSA)Ω(W−MSA)=4hwC2+2(hw)2C,=4hwC2+2M2hwC,

将Transformer从语言转换到视觉的挑战来自于两个领域之间的差异,例如视觉实体的尺度变化较大,图像中的像素相对于文本中的文字分辨率较高。
为了解决这些差异,提出了一个分层Transformer,其表示由Shifted窗口计算。移位窗口方案通过将自注意力计算限制在不重叠的局部窗口,同时允许跨窗口连接,从而带来更高的效率。这种分层架构具有在各种尺度下建模的灵活性,并且具有与图像大小相关的线性计算复杂度。
Twins
[2104.13840] Twins: Revisiting the Design of Spatial Attention in Vision Transformers (arxiv.org)


在这项工作中,重新审视了空间注意力的设计,并证明了一个精心设计但简单的空间注意力机制与最先进的方案相比具有良好的性能。因此,我们提出了两种视觉转换器结构,即Twins - PCPVT和TwinsSVT。我们提出的架构高效且易于实现,只涉及在现代深度学习框架中高度优化的矩阵乘法。更重要的是,所提出的架构在包括图像级cla在内的广泛的视觉任务上取得了优异的性能
此外随着时间发展,目前已经有了空间注意力,通道注意力等等可以用于2D数据的注意力模型.但是基本思想是类似的.
参考资料
- Relative position embedding - 知乎 (zhihu.com)
- [1803.02155] Self-Attention with Relative Position Representations (arxiv.org)
- Relative Positional Embedding | Chao Yang (placebokkk.github.io)
- Improve Transformer Models with Better Relative Position Embeddings (aclanthology.org)
- 让研究人员绞尽脑汁的Transformer位置编码 - 知乎 (zhihu.com)
- 《A survey of the Vision Transformers and its CNN-Transformer based Variants》第一期 - 知乎 (zhihu.com)
如有疑问,欢迎各位交流!
服务器配置
宝塔:宝塔服务器面板,一键全能部署及管理
云服务器:阿里云服务器
Vultr服务器
GPU服务器:Vast.ai
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容








所有评论(0)