本文学习的是从零开始手把手搭建Vision Transformers(Pytorch版本)_从0搭建transfomer实现cv任务

在这里插入图片描述

首先，输入图像（a）先被切割成大小相等的patch 子图片，然后每个子图片均被放入到Linear Embedding 中，对每个图片向量做一个全连接操作，做transformer输入的前处理从Linear Embedding层出来后，加入Positonal encoding 将各个patch在图像中的相对位置信息考虑进去，后面就是transformer Encoder的过程，在之后加入MLP的分类head，输出图像的分类。

transformer开始是用于NLP这种序列化数据，因此第一步就是将图像序列化

步骤一：图像序列化

以一张图为例

在这里插入图片描述

将每个（1x28x28）的图像分成7x7块，每块大小是4x4（如果不能完全整除分块，需要对图像padding填充），这样我们能从单个图像中获得49个子图像。将原图重塑成：（N,49,16）即N个batch，49个子块，每块4*4。

请注意，虽然每个子图大小为 1x4x4 ，但我们将其展平为 16 维向量。此外，MNIST只有一个颜色通道。如果有多个颜色通道，它们也会被展平到矢量中。

代码如下：

class MyViT(nn.Module):
    def __init__(self, input_shape, n_patches=7):    
        # Super constructor        
        super(MyViT, self).__init__()
        
        # Input and patches sizes        
        self.input_shape = input_shape#输入尺寸这里是1，128，128        
        self.n_patches = n_patches#patch数这里是7        
        assert input_shape[1] % n_patches == 0, "Input shape not entirely divisible by number of patches"#若不能整除，报错        
        assert input_shape[2] % n_patches == 0, "Input shape not entirely divisible by number of patches"#若不能整除，报错

    def forward(self, images):    
        # Dividing images into patches#分割为子块        
        n, c, w, h = images.shape#获取输入图像尺寸，n为batch数，c为通道数，w为宽，h为高        
        patches = images.reshape(n, self.n_patches ** 2, self.input_d)#变为(n,49,16)        
        return patches #返回patch数目

在这里插入图片描述

我们就把一张图像变为49行16列的维度，每一行代表一个子图对其已经进行打平成为一维向量，然后对通过一个线性映射来改变维度，线性映射可以映射到任意向量大小，我们向类构造函数添加一个hidden_d参数，用于“隐藏维度”。这里，使用隐藏维度为8，这样我们将每个 16 维patch映射到一个 8 维patch。

class MyViT(nn.Module):
    def __init__(self, input_shape, n_patches=7, hidden_d=8):    
        # Super constructor        
        super(MyViT, self).__init__()
        
        # Input and patches sizes        
        self.input_shape = input_shape        
        self.n_patches = n_patches        
        assert input_shape[1] % n_patches == 0, "Input shape not entirely divisible by number of patches"        
        assert input_shape[2] % n_patches == 0, "Input shape not entirely divisible by number of patches"        
        self.hidden_d = hidden_d#这是隐藏层维度
        
        # 1) Linear mapper#线性映射        
        self.input_d = int(input_shape[0] * self.patch_size[0] * self.patch_size[1])#输入维度，这里就是1*4*4=16
#若是三维的即3*4*4，将三通道也打平为一维序列        
        self.linear_mapper = nn.Linear(self.input_d, self.hidden_d)#线性映射，可将维度进行调整，其本质为一个全连接层
        
    def forward(self, images):        
    # Dividing images into patches        
    n, c, w, h = images.shape        
    patches = images.reshape(n, self.n_patches ** 2, self.input_d)         
    # Running linear layer for tokenization #将        
    tokens = self.linear_mapper(patches)#进行线性变换维度变换为，(n,49,8)从开始16变换为8
    
    return tokens

在这里插入图片描述

这里分类v是在位置嵌入之后的，本人认为也应该是这样因为classification token为分类标记不需要添加位置信息因此应该先位置嵌入然后再添加classification token

在添加隐藏层后，为了完成分类任务，我们需要添加分类标记，现在可以向我们的模型添加一个参数将我们的 (N, 49, 8)张量转换为 (N, 50, 8) 张量（将特殊标记添加到每个序列）

class MyViT(nn.Module):
    def __init__(self, input_shape, n_patches=7, hidden_d=8, n_heads=2, out_d=10):   
        # Super constructor        
        super(MyViT, self).__init__()
        
        # Input and patches sizes        
        self.input_shape = input_shape        
        self.n_patches = n_patches        
        self.n_heads = n_heads        
        assert input_shape[1] % n_patches == 0, "Input shape not entirely divisible by number of patches"        
        assert input_shape[2] % n_patches == 0, "Input shape not entirely divisible by number of patches"        
        self.hidden_d = hidden_d
        
        # 1) Linear mapper        
        self.input_d = int(input_shape[0] * self.patch_size[0] * self.patch_size[1])        
        self.linear_mapper = nn.Linear(self.input_d, self.hidden_d)
        
        # 2) Classification token        
        self.class_token = nn.Parameter(torch.rand(1, self.hidden_d))#参数，(1,8)的
        
    def forward(self, images):    
        # Dividing images into patches        
        n, c, w, h = images.shape        
        patches = images.reshape(n, self.n_patches ** 2, self.input_d)       
         # Running linear layer for tokenization       
        tokens = self.linear_mapper(patches)        
        # Adding classification token to the tokens将分类标记放入token中        
        tokens = torch.stack([torch.vstack((self.class_token, tokens[i])) for i in range(len(tokens))])
'''
vstack 是一个用于垂直堆叠两个张量的操作。在这里，self.class_token 和 tokens[i] 被垂直堆叠在一起。
这意味着我们将 class_token 放在每个 tokens[i] 的最上面，形成一个新的张量，该张量的第一行是 class_token，
而后面的行是 tokens[i] 的元素。
现在token[0]为class_token
而后面的为每个子图的token
举一个例子哦
tokens = torch.tensor([
    [0.1, 0.2, 0.3],  # token 0    
    [0.4, 0.5, 0.6],  # token 1    
    [0.7, 0.8, 0.9]   # token 2
])
class_token = torch.tensor([1.0, 1.0, 1.0]) 
现在进行该步骤
[torch.vstack((self.class_token, tokens[i])) for i in range(len(tokens))]
就会变为
tokens = torch.tensor([
    [1.0, 1.0, 1.0],  # token 0    
    [0.1, 0.2, 0.3],  # token 1    
    [0.4, 0.5, 0.6],  # token 2    
    [0.7, 0.8, 0.9]   # token 3
])
'''
        return tokens

请注意，这里 (N,49,8) → (N,50,8) 实现方式可能不是最佳的。另外，请注意**分类标记需要放在每个序列的第一个标记位。**当我们完成最终 MLP 时，需要对应到对应的位置上。

添加位置编码

位置编码参见transformer模型中位置标明的输入，虽然理论上可以学习这种位置嵌入，但是这块也有人研究过，建议我们可以只添加正弦和余弦波。

def get_positional_embeddings(sequence_length, d):
    result = torch.ones(sequence_length, d)#sequence_length子图数量，d子图特征    
    for i in range(sequence_length):#遍历每张子图    
        for j in range(d):#遍历每个特征       
            result[i][j] = np.sin(i / (10000 ** (j / d))) if j % 2 == 0 else np.cos(i / (10000 ** ((j - 1) / d)))
#若j为偶数则用sin方法，若j为奇数则cos方法
    return resul#维度最后不变

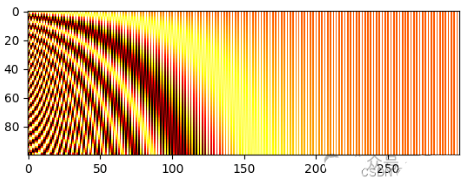
在这里插入图片描述

在这里插入图片描述

从绘制的热图中，看到所有“水平线”都彼此不同，因此可以区分样本位置。

现在可以在线性映射和添加分类标记后将位置编码添加到模型中：

class MyViT(nn.Module):
    def __init__(self, input_shape, n_patches=7, hidden_d=8, n_heads=2, out_d=10):     
        # Super constructor        
        super(MyViT, self).__init__()
        
        # Input and patches sizes        
        self.input_shape = input_shape        
        self.n_patches = n_patches        
        self.n_heads = n_heads        
        assert input_shape[1] % n_patches == 0, "Input shape not entirely divisible by number of patches"        
        assert input_shape[2] % n_patches == 0, "Input shape not entirely divisible by number of patches"        
        self.patch_size = (input_shape[1] / n_patches, input_shape[2] / n_patches)        self.hidden_d = hidden_d
        
        # 1) Linear mapper        
        self.input_d = int(input_shape[0] * self.patch_size[0] * self.patch_size[1])        
        self.linear_mapper = nn.Linear(self.input_d, self.hidden_d)
        
        # 2) Classification token        
        self.class_token = nn.Parameter(torch.rand(1, self.hidden_d))
        
        # 3) Positional embedding        
        # (In forward method)
        


    def forward(self, images):    
        # Dividing images into patches        
        n, c, w, h = images.shape        
        patches = images.reshape(n, self.n_patches ** 2, self.input_d)
        
        # Running linear layer for tokenization        
        tokens = self.linear_mapper(patches)
        
        # Adding classification token to the tokens        
        tokens = torch.stack([torch.vstack((self.class_token, tokens[i])) for i in range(len(tokens))])
        
        # Adding positional embedding        
        tokens += get_positional_embeddings(self.n_patches ** 2 + 1, self.hidden_d).repeat(n, 1, 1)
#position_embedding维度为(50,8)因为有n个，因此要进行重复变为(n,50,8)，
#有tokens维度(n,50,8)这样tokens和position_embedding进行对应位置元素相加，即位置嵌入，逐元素相加

        return tokens

img

img

img

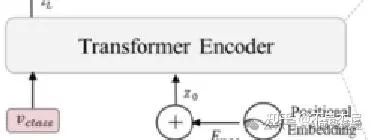
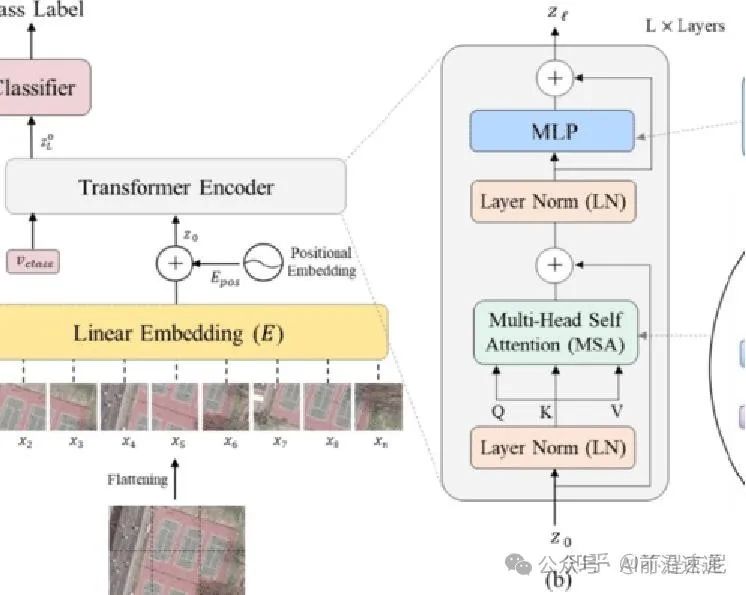
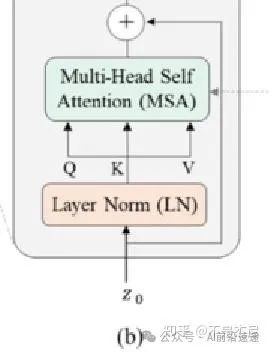
LN, MSA和残差连接

这是最LN, MSA和残差连接复杂的一步。我们需要先对tokens做层归一化，然后应用多头注意力机制，最后添加一个残差连接（连接LN 之前的输入和多头注意力之后的输出）。

我们通常将LN应用于 (N, d) 输入，其中 d 是维度。直到自己实现 ViT，才发现nn.LayerNorm可以应用于多个维度。

img

通过 LN 运行 (N, 50, 8) 张量后，每个 50x8 矩阵的均值为 0 和标准差为 1，维度不变。

多头自注意力

img

img

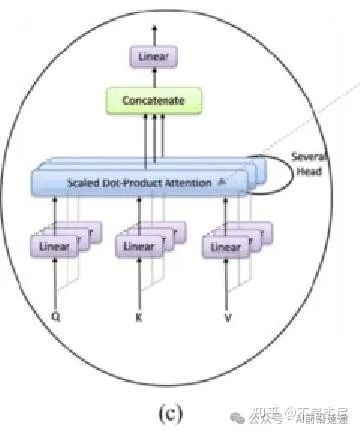
我们现在需要实现架构图的子图c。这里就是多头注意力机制对于单个图像，我们希望每个patch都根据与其他patch的某种相似性度量来更新。通过将每个patch（示例中现在是一个 8 维向量）线性映射到 3 个不同的向量：q、k和v（查询、键、值）。然后，对于单个patch，我们将计算其q向量与所有k个向量之间的点积(即相似度)，除以这些向量维度的平方根d，对计算结果softmax激活(获得相似度的概率)，最后将计算结果与不同k向量相关联的v向量相乘，简单的理解也可以类似搜索引擎，你输入的问题就是Q，与索引键K进行匹配若比较类似则说明K对应的V是你所搜索的信息其权重应该高一点。整个计算公式如下。

img

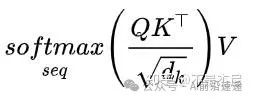
通过这种方式，每个patch获得一个新值，该新值为与其他patch的相似性（在线性映射到q、k和v之后）。整个过程为单头，多头则重复多次整个过程。获得所有结果后，将它们通过线性层连接在一起。

因此为 MSA 创建一个新类：

class MyMSA(nn.Module):
    def __init__(self, d, n_heads=2):    
        super(MyMSA, self).__init__()        
        self.d = d#维度
#在多头自注意力中，输入的特征维度需要在每个头之间进行均匀分配
        self.n_heads = n_heads#自注意力头数
        
        assert d % n_heads == 0, f"Can't divide dimension {d} into {n_heads} heads"#若
        
        d_head = int(d / n_heads)#每个头的维度
#在自注意力机制中，我们需要为每个输入向量生成查询、键和值。每个头（head）都有自己独立的参数来生成这些向量，
#这样每个头能够学习到不同的特征。
        self.q_mappings = [nn.Linear(d_head, d_head) for _ in range(self.n_heads)]        
        self.k_mappings = [nn.Linear(d_head, d_head) for _ in range(self.n_heads)]        
        self.v_mappings = [nn.Linear(d_head, d_head) for _ in range(self.n_heads)]        
        self.d_head = d_head        
        self.softmax = nn.Softmax(dim=-1)
        
    def forward(self, sequences):    
        # Sequences has shape (N, seq_length, token_dim)        
        # We go into shape    (N, seq_length, n_heads, token_dim / n_heads)        
        # And come back to    (N, seq_length, item_dim)  (through concatenation)        
        result = []        
        for sequence in sequences:         
            seq_result = []            
            for head in range(self.n_heads):#遍历每个头           
                q_mapping = self.q_mappings[head]#每个头的q                
                k_mapping = self.k_mappings[head]#每个头的k                
                v_mapping = self.v_mappings[head]#每个头的v
                
                seq = sequence[:, head * self.d_head: (head + 1) * self.d_head]#按head进行头数进行分段                
                q, k, v = q_mapping(seq), k_mapping(seq), v_mapping(seq)
                
                attention = self.softmax(q @ k.T / (self.d_head ** 0.5))#求相似度                
                seq_result.append(attention @ v)#结果       
            result.append(torch.hstack(seq_result))
'''
torch.hstack() 是 PyTorch 中用于进行张量水平堆叠的函数。
它的作用是将多个相同形状的张量在水平方向上连接（拼接）在一起。
result.append(torch.hstack(seq_result)) 的核心作用在于将来自不同注意力头的加权输出合并成一个更大的张量。
这种拼接操作不仅方便后续的特征处理，还能够增强模型的表达能力，使模型能够从多个头中综合信息，提高模型的性能。
'''
        return torch.cat([torch.unsqueeze(r, dim=0) for r in result])#将多个注意力头提取的特征进行组合

由于输入是大小为 (N, 50, 8) 的序列，我们使用 2 个头，因此我们将在某些时候有 (N, 50, 2, 4) 张量，使用nn.Linear(4, 4 )模块，然后在连接后返回到 (N, 50, 8) 张量。另，使用循环并不是计算多头自注意力的最有效方法，但代码更清晰。

class MyViT(nn.Module):
    def __init__(self, input_shape, n_patches=7, hidden_d=8, n_heads=2, out_d=10):     
        # Super constructor        
        super(MyViT, self).__init__()
        
        # Input and patches sizes        
        self.input_shape = input_shape        
        self.n_patches = n_patches        
        self.n_heads = n_heads        
        assert input_shape[1] % n_patches == 0, "Input shape not entirely divisible by number of patches"        
        assert input_shape[2] % n_patches == 0, "Input shape not entirely divisible by number of patches"        self.patch_size = (input_shape[1] / n_patches, input_shape[2] / n_patches)        self.hidden_d = hidden_d
        
        # 1) Linear mapper        
        self.input_d = int(input_shape[0] * self.patch_size[0] * self.patch_size[1])        
        self.linear_mapper = nn.Linear(self.input_d, self.hidden_d)
        
        # 2) Classification token        
        self.class_token = nn.Parameter(torch.rand(1, self.hidden_d))
        
        # 3) Positional embedding        
        # (In forward method)
        
        # 4a) Layer normalization 1        
        self.ln1 = nn.LayerNorm((self.n_patches ** 2 + 1, self.hidden_d))
        
        # 4b) Multi-head Self Attention (MSA) and classification token        
        self.msa = MyMSA(self.hidden_d, n_heads)#多头注意力
        


    def forward(self, images):    
        # Dividing images into patches        
        n, c, w, h = images.shape        
        patches = images.reshape(n, self.n_patches ** 2, self.input_d)
        
        # Running linear layer for tokenization        
        tokens = self.linear_mapper(patches)
        
        # Adding classification token to the tokens        
        tokens = torch.stack([torch.vstack((self.class_token, tokens[i])) for i in range(len(tokens))])
        
        # Adding positional embedding        
        tokens += get_positional_embeddings(self.n_patches ** 2 + 1, self.hidden_d).repeat(n, 1, 1)
        
        # TRANSFORMER ENCODER BEGINS ###################################        
        # NOTICE: MULTIPLE ENCODER BLOCKS CAN BE STACKED TOGETHER ######        
        # Running Layer Normalization, MSA and residual connection        
        out = tokens + self.msa(self.ln1(tokens))#token通过线性层再进行多头注意力，最后与原来的token连接，进行残差连接
        
        return out

将添加一个残差连接，它将我们的原始 (N, 50, 8) 张量添加到在 LN 和 MSA 之后获得的 (N, 50, 8)。

img

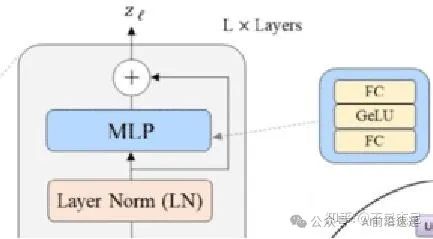
再进行一次layernorm以及一次MLP

class MyViT(nn.Module):
    def __init__(self, input_shape, n_patches=7, hidden_d=8, n_heads=2, out_d=10):    
        # Super constructor        
        super(MyViT, self).__init__()
        
        # Input and patches sizes        
        self.input_shape = input_shape        
        self.n_patches = n_patches        
        self.n_heads = n_heads        
        assert input_shape[1] % n_patches == 0, "Input shape not entirely divisible by number of patches"        
        assert input_shape[2] % n_patches == 0, "Input shape not entirely divisible by number of patches"        
        self.patch_size = (input_shape[1] / n_patches, input_shape[2] / n_patches)        
        self.hidden_d = hidden_d
        
        # 1) Linear mapper        
        self.input_d = int(input_shape[0] * self.patch_size[0] * self.patch_size[1])        
        self.linear_mapper = nn.Linear(self.input_d, self.hidden_d)
        
        # 2) Classification token        
        self.class_token = nn.Parameter(torch.rand(1, self.hidden_d))
        
        # 3) Positional embedding        
        # (In forward method)
        
        # 4a) Layer normalization 1        
        self.ln1 = nn.LayerNorm((self.n_patches ** 2 + 1, self.hidden_d))
        
        # 4b) Multi-head Self Attention (MSA) and classification token        
        self.msa = MyMSA(self.hidden_d, n_heads)
        
        # 5a) Layer normalization 2          
        self.ln2 = nn.LayerNorm((self.n_patches ** 2 + 1, self.hidden_d))#第二层的Layer-normal
        
        # 5b) Encoder MLP 进行多层感知        
        self.enc_mlp = nn.Sequential(            
            nn.Linear(self.hidden_d, self.hidden_d),#线性层            
            nn.ReLU()#激活函数        
        )


    def forward(self, images):    
        # Dividing images into patches        
        n, c, w, h = images.shape        
        patches = images.reshape(n, self.n_patches ** 2, self.input_d)
        
        # Running linear layer for tokenization        
        tokens = self.linear_mapper(patches)
       
        # Adding classification token to the tokens        
        tokens = torch.stack([torch.vstack((self.class_token, tokens[i])) for i in 
        range(len(tokens))])
        
        # Adding positional embedding        
        tokens += get_positional_embeddings(self.n_patches ** 2 + 1, self.hidden_d).repeat(n, 1, 1)
        
        # TRANSFORMER ENCODER BEGINS ###################################        
        # NOTICE: MULTIPLE ENCODER BLOCKS CAN BE STACKED TOGETHER ######        
        # Running Layer Normalization, MSA and residual connection        
        out = tokens + self.msa(self.ln1(tokens))
        
        # Running Layer Normalization, MLP and residual connection        
        out = out + self.enc_mlp(self.ln2(out))        
        # TRANSFORMER ENCODER ENDS   ###################################
        
        return out

最后进行分类MLP

我们可以从 N 个序列中只提取分类标记（第一个标记），与添加分类标签的位置对应，并使用每个标记得到 N 个分类。由于我们决定每个标记是一个 8 维向量，并且由于我们有 10 个可能的数字，我们可以将分类 MLP 实现为一个简单的 8x10 矩阵，并使用 SoftMax 函数激活。即每张子图是8个特征的(本来是16个特征我们经过线性变换变为8个)每张子图生成类别的概率一共有10个数字可能，因此分类MLP首先为一个简单的8X10矩阵

class MyViT(nn.Module):
    def __init__(self, input_shape, n_patches=7, hidden_d=8, n_heads=2, out_d=10):    
        # Super constructor        
        super(MyViT, self).__init__()
        
        # Input and patches sizes        
        self.input_shape = input_shape        
        self.n_patches = n_patches        
        self.n_heads = n_heads        
        assert input_shape[1] % n_patches == 0, "Input shape not entirely divisible by number of patches"        
        assert input_shape[2] % n_patches == 0, "Input shape not entirely divisible by number of patches"        
        self.patch_size = (input_shape[1] / n_patches, input_shape[2] / n_patches)        
        self.hidden_d = hidden_d
        
        # 1) Linear mapper        
        self.input_d = int(input_shape[0] * self.patch_size[0] * self.patch_size[1])        
        self.linear_mapper = nn.Linear(self.input_d, self.hidden_d)
        
        # 2) Classification token        
        self.class_token = nn.Parameter(torch.rand(1, self.hidden_d))
        
        # 3) Positional embedding        
        # (In forward method)
        
        # 4a) Layer normalization 1        
        self.ln1 = nn.LayerNorm((self.n_patches ** 2 + 1, self.hidden_d))
        
        # 4b) Multi-head Self Attention (MSA) and classification token        
        self.msa = MyMSA(self.hidden_d, n_heads)
        
        # 5a) Layer normalization 2        
        self.ln2 = nn.LayerNorm((self.n_patches ** 2 + 1, self.hidden_d))
        
        # 5b) Encoder MLP 编码MLP        
        self.enc_mlp = nn.Sequential(            
            nn.Linear(self.hidden_d, self.hidden_d),            
            nn.ReLU()        
        )
        
        # 6) Classification MLP 分类MLP        
        self.mlp = nn.Sequential(            
            nn.Linear(self.hidden_d, out_d),#隐藏层8，输出层10.一个N是8个特征                   
            nn.Softmax(dim=-1)        
        )
        
    def forward(self, images):    
        # Dividing images into patches        
        n, c, w, h = images.shape        
        patches = images.reshape(n, self.n_patches ** 2, self.input_d)
        
        # Running linear layer for tokenization        
        tokens = self.linear_mapper(patches)
        
        # Adding classification token to the tokens        
        tokens = torch.stack([torch.vstack((self.class_token, tokens[i])) for i in range(len(tokens))])
        
        # Adding positional embedding        
        tokens += get_positional_embeddings(self.n_patches ** 2 + 1, self.hidden_d).repeat(n, 1, 1)
        
        # TRANSFORMER ENCODER BEGINS ###################################        
        # NOTICE: MULTIPLE ENCODER BLOCKS CAN BE STACKED TOGETHER ######        
        # Running Layer Normalization, MSA and residual connection        
        out = tokens + self.msa(self.ln1(tokens))
        
        # Running Layer Normalization, MLP and residual connection        
        out = out + self.enc_mlp(self.ln2(out))        
        # TRANSFORMER ENCODER ENDS   ###################################
        
        # Getting the classification token only        
        out = out[:, 0]#获得分类标记token
        
        return self.mlp(out)#进行分类

我们模型的输出现在是一个 (N, 10) 张量，一张图10种类别的可能性
完整测试脚本如下：

# import torch
#
# # 假设输入 tokens 的维度为 (N, 49, 8)
# N = 2  # 假设批量大小为 2
# num_tokens = 49  # 每个样本中 token 的数量
# feature_size = 8  # 所有 tokens 的特征维度
#
# # 创建随机输入 tokens，形状为 (N, num_tokens, feature_size)
# tokens = torch.rand(N, num_tokens, feature_size)
#
# # 定义 class token（只有一行，与 token 的特征维度一致）
# class_token = torch.ones(1, feature_size)  # 形状为 (1, 8)
#
# # 在每个 token 上方添加 class token
# # 使用列表推导式
# tokens_with_class_token = torch.stack(
#     [torch.vstack((class_token, tokens[0]))]
# )
#
# # 输出结果的形状
# print("Input tokens shape:", tokens.shape)  # (N, 49, 8)
# print("Class token shape:", class_token.shape)  # (1, 8)
# print("Result tokens with class token shape:", tokens_with_class_token.shape)  # (N, 49, 2, 8)
#
# # 验证是否在每个 token 上方添加了 class token
#
# for i in range(N):
#     print(f"Sample {i} tokens with class token:")
#     print(tokens_with_class_token[i])
# import torch
#
# def get_positional_embeddings(sequence_length, d):
#     result = torch.ones(sequence_length, d)  # 初始化全1的张量
#     for i in range(sequence_length):  # 遍历每个位置
#         for j in range(d):  # 遍历每个特征
#             if j % 2 == 0:
#                 result[i][j] = torch.sin(torch.tensor(i) / (10000 ** (j / d)))  # 偶数索引使用sin
#             else:
#                 result[i][j] = torch.cos(torch.tensor(i) / (10000 ** ((j - 1) / d)))  # 奇数索引使用cos
#     return result  # 返回嵌入矩阵
#
# # 示例调用
# sequence_length = 10  # 例如有10个子图
# d = 8  # 每个子图的特征维度
# positional_embeddings = get_positional_embeddings(sequence_length, d)
# print(positional_embeddings.shape)
import torch
import torch.nn as nn
import numpy as np


class MyMSA(nn.Module):
    def __init__(self, d, n_heads=2):    
        super(MyMSA, self).__init__()        
        self.d = d        
        self.n_heads = n_heads        
        assert d % n_heads == 0, f"Can't divide dimension {d} into {n_heads} heads"        
        d_head = int(d / n_heads)
        
        self.q_mappings = nn.ModuleList([nn.Linear(d_head, d_head) for _ in range(self.n_heads)])        
        self.k_mappings = nn.ModuleList([nn.Linear(d_head, d_head) for _ in range(self.n_heads)])        
        self.v_mappings = nn.ModuleList([nn.Linear(d_head, d_head) for _ in range(self.n_heads)])        
        self.d_head = d_head        
        self.softmax = nn.Softmax(dim=-1)
        
    def forward(self, sequences):    
        result = []        
        for sequence in sequences:        
            seq_result = []            
            for head in range(self.n_heads):            
                q_mapping = self.q_mappings[head]                
                k_mapping = self.k_mappings[head]                
                v_mapping = self.v_mappings[head]
                
                # Extract head-specific part                
                seq = sequence[:, head * self.d_head: (head + 1) * self.d_head]                
                q, k, v = q_mapping(seq), k_mapping(seq), v_mapping(seq)
                
                attention = self.softmax(q @ k.T / (self.d_head ** 0.5))                
                seq_result.append(attention @ v)            
           result.append(torch.hstack(seq_result))        
       return torch.cat([torch.unsqueeze(r, dim=0) for r in result])


def get_positional_embeddings(sequence_length, d):
    result = torch.ones(sequence_length, d)    
    for i in range(sequence_length):        
        for j in range(d):       
            result[i][j] = np.sin(i / (10000 ** (j / d))) if j % 2 == 0 else np.cos(i / (10000 ** ((j - 1) / d)))    
    return result
    

class MyViT(nn.Module):
    def __init__(self, input_shape, n_patches=7, hidden_d=8, n_heads=2, out_d=10):    
        super(MyViT, self).__init__()        
        self.input_shape = input_shape#(1,28,28)        
        self.n_patches = n_patches        
        self.n_heads = n_heads        
        print(input_shape)#为28，28        
        assert input_shape[1] % n_patches == 0, "Input shape not entirely divisible by number of patches"        
        assert input_shape[2] % n_patches == 0, "Input shape not entirely divisible by number of patches"        
        self.patch_size = (input_shape[1] // n_patches, input_shape[2] // n_patches)        
        self.hidden_d = hidden_d
        
        # 1) Linear mapper        
        self.input_d = int(input_shape[0] * self.patch_size[0] * self.patch_size[1])#这应该为16，通道数1*子图宽4*子图高4
        
        self.linear_mapper = nn.Linear(self.input_d, self.hidden_d)
        
        # 2) Classification token        
        self.class_token = nn.Parameter(torch.rand(1, self.hidden_d))
        
        # 4) Layer normalization 1        
        self.ln1 = nn.LayerNorm((self.n_patches ** 2 + 1, self.hidden_d))
        
        # 4b) Multi-head Self Attention (MSA)        
        self.msa = MyMSA(self.hidden_d, n_heads)
        
        # 5) Layer normalization 2        
        self.ln2 = nn.LayerNorm((self.n_patches ** 2 + 1, self.hidden_d))
        
        # 5b) Encoder MLP        
        self.enc_mlp = nn.Sequential(      
            nn.Linear(self.hidden_d, self.hidden_d),            
            nn.ReLU()        
        )
        
        # 6) Classification MLP        
        self.mlp = nn.Sequential(       
            nn.Linear(self.hidden_d, out_d),            
            nn.Softmax(dim=-1)        
        )
        
    def forward(self, images):    
        # Dividing images into patches        
        n, c, w, h = images.shape#1,1,28,28        
        patches = images.reshape(n, self.n_patches ** 2, self.input_d)#1，49，16        
        print(f"input_d:{self.input_d}")#16        
        print(f"Patches shape1: {patches.shape}")  # Output after patching
        
        # Running linear layer for tokenization 线性层        
        tokens = self.linear_mapper(patches)#(1,49,16)变为(1,49,8)        
        print(f"Tokens shape after linear mapping: {tokens.shape}")  # Output after linear mapping
        
        # Adding classification token to the tokens        
        tokens = torch.stack([torch.vstack((self.class_token, tokens[i])) for i in range(len(tokens))])#增加分类标记(1,50,8)        
        print(f"Tokens shape after adding classification token: {tokens.shape}")  # Output after adding classification token
        
        # Adding positional embedding        
        tokens += get_positional_embeddings(self.n_patches ** 2 + 1, self.hidden_d).repeat(n, 1, 1)#嵌入位置信息 (1,50,8)        
        print(f"Tokens shape after adding positional embedding: {tokens.shape}")  # Output after adding positional embeddings
        
        # TRANSFORMER ENCODER BEGINS ###################################        
        # Running Layer Normalization, MSA and residual connection        
        out = tokens + self.msa(self.ln1(tokens))#多头注意力(1,50,8)        
        print(f"Output shape after MSA: {out.shape}")  # Output after MSA
        
        # Running Layer Normalization, MLP and residual connection        
        out = out + self.enc_mlp(self.ln2(out))#经过Layer-norm MLP 残差 (1,50,8)        
        print(f"Output shape after MLP: {out.shape}")  # Output after MLP        
        # TRANSFORMER ENCODER ENDS   ###################################
        
        # Getting the classification token only        
        out = out[:, 0]#输出(n,8)一个图，8个特征标记，最后用mlp生成(n,10)一张图可能为10个数字可能        
        print(f"Final output shape (classification token): {out.shape}")  # Shape of the final output
        
        return self.mlp(out)
        

# Define input shape (batch size, channels, width, height)
input_shape = (1, 28, 28)
input_image_shape=(1,1,28,28)
# Create model
model = MyViT(input_shape=input_shape)

# Create random input tensor with shape (1, 1, 28, 28)
images = torch.rand(input_image_shape)

# Forward pass
output = model(images)
print(f"10类 output：{output.shape}")

可以运行一下看看维度变化

结果应该为：

img

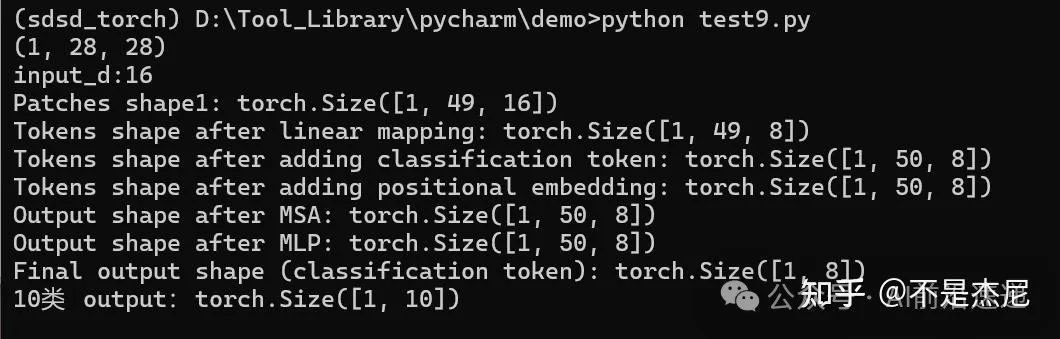
如何学习大模型

下面这些都是我当初辛苦整理和花钱购买的资料，现在我已将重要的AI大模型资料包括市面上AI大模型各大白皮书、AGI大模型系统学习路线、AI大模型视频教程、实战学习，等录播视频免费分享出来，需要的小伙伴可以扫取。

现在社会上大模型越来越普及了，已经有很多人都想往这里面扎，但是却找不到适合的方法去学习。

作为一名资深码农，初入大模型时也吃了很多亏，踩了无数坑。现在我想把我的经验和知识分享给你们，帮助你们学习AI大模型，能够解决你们学习中的困难。

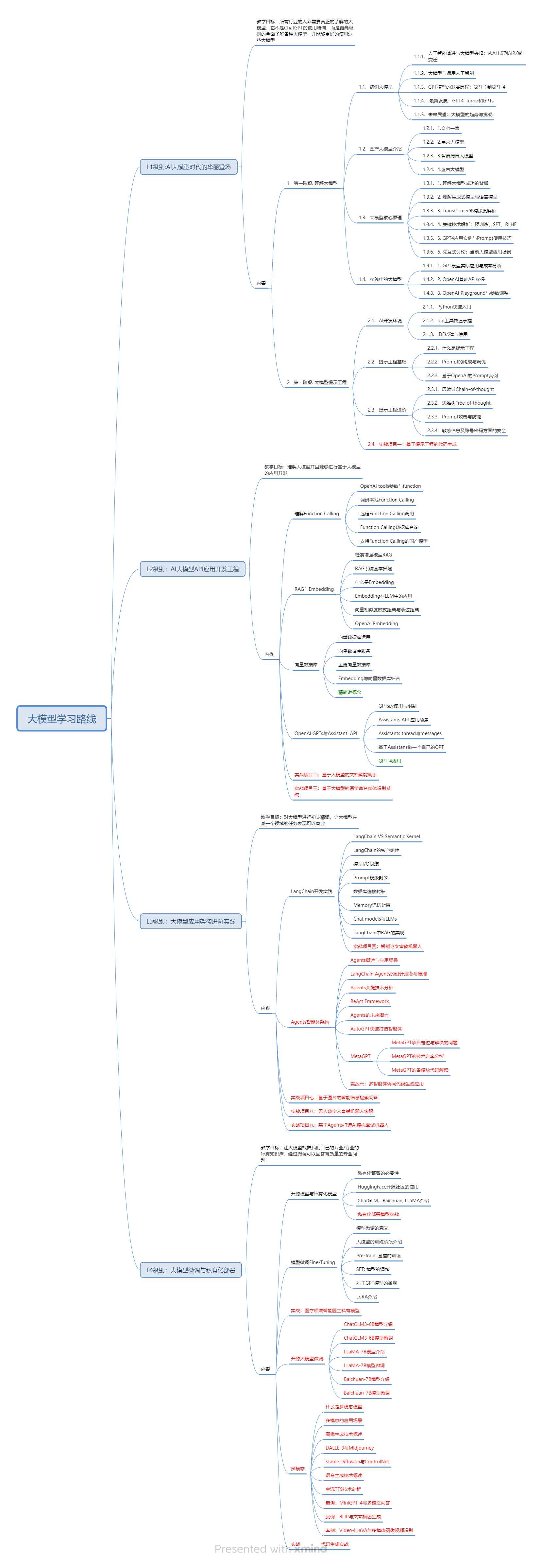
一、AGI大模型系统学习路线

很多人学习大模型的时候没有方向，东学一点西学一点，像只无头苍蝇乱撞，我下面分享的这个学习路线希望能够帮助到你们学习AI大模型。

在这里插入图片描述

二、AI大模型视频教程

在这里插入图片描述

三、AI大模型各大学习书籍!

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

四、AI大模型各大场景实战案例

在这里插入图片描述

五、AI大模型面试题库

在这里插入图片描述

五、结束语

学习AI大模型是当前科技发展的趋势，它不仅能够为我们提供更多的机会和挑战，还能够让我们更好地理解和应用人工智能技术。通过学习AI大模型，我们可以深入了解深度学习、神经网络等核心概念，并将其应用于自然语言处理、计算机视觉、语音识别等领域。同时，掌握AI大模型还能够为我们的职业发展增添竞争力，成为未来技术领域的领导者。

再者，学习AI大模型也能为我们自己创造更多的价值，提供更多的岗位以及副业创收，让自己的生活更上一层楼。

因此，学习AI大模型是一项有前景且值得投入的时间和精力的重要选择。

# transformer # 人工智能 # 深度学习
Logo
尧米AI

尧米是由西云算力与CSDN联合运营的AI算力和模型开源社区品牌，为基于DaModel智算平台的AI应用企业和泛AI开发者提供技术交流与成果转化平台。

更多推荐

cover

windows本地部署vllm,运行deepseek大模型

avatar 尧米AI
cover

本地部署deepseek大模型后使用c# winform调用（可离线）

avatar 尧米AI
cover

LightRAG+Ollama本地部署

avatar 尧米AI